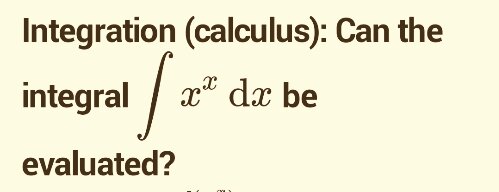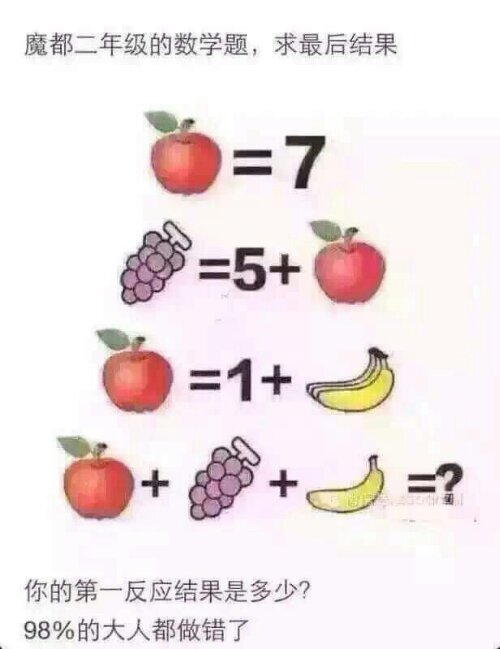Month: October 2015

Calculus World Cup

Just to share this news: 

The National Taiwan University is holding the first ever Calculus World Cup (CWC) in February 2016. It’s the first time students from global top universities will be able to compete over Calculus in e-sports. The competition will be held on PaGamO – a social online gaming platform for education. The top 12 teams will be invited to Taiwan for the final round, and great prizes with a value of over $70,000 await the finalists! 
Official website: http://cwc.pagamo.com.tw

Registration: https://pagamo.com.tw/calculus_cup

Facebook: https://www.facebook.com/PaGamo.glo

Contractible space as Codomain implies any two maps Homotopic

Click here for: Free Personality Quiz

Recall that a space Y is contractible if the identity map \text{id}_Y is homotopic to a constant map. Let Y be contractible space and let X be any space. Then, for any maps f,g: X\to Y, f\simeq g.

Proof: Let Y be a contractible space and let X be any space. \text{id}_Y\simeq c, where c is a constant map. There exists a map F: Y\times [0,1]\to Y such that F(y,0)=\text{id}_Y(y)=y, for y\in Y. F(y,1)=c(y)=b for some point b\in Y.

Let f,g: X\to Y be any two maps. Consider G:X\times [0,1]\to Y where G(x,t)=\begin{cases} F(f(x),2t),&\ \ \ \text{for}\ 0\leq t\leq 1/2\\ F(g(x),-2t+2),&\ \ \ \text{for}\ \frac 12<t\leq 1 \end{cases}

When t=\frac 12, F(f(x),1)=b, F(g(x),1)=b. Therefore G is cts.

G(x,0)=F(f(x),0)=f(x),

G(x,1)=F(g(x),0)=g(x).

Therefore f\simeq g.

Outer measure of Symmetric Difference Zero implies Measurability

Free Career Quiz: Please help to do!

Just came across this neat beginner’s Lebesgue Theory question. As students of analysis know, just to show a set is measurable is no easy feat. The usual way is to use the Caratheodory definition, where  a set E is said to be measurable if for any set A, m^*(A)=m^*(A\cap E)+m^*(A\cap E^c). This can be quite tedious.

Question: Suppose E is a Lebesgue measurable set and let F be any subset of \mathbb{R} such that m^*(E\Delta F)=0 (Symmetric Difference is Zero). Show that F is measurable.

The short way to do this is to note that m^*(E\Delta F)=0 implies m^*(E\setminus F)=0, and m^*(F\setminus E)=0. This in turn (using a lemma that any set with outer measure zero is measurable) implies the measurability of E\setminus F and \setminus F\setminus E.

Next comes the critical observation: \boxed{E\cap F=E\setminus (E\setminus F)=E\cap (E\setminus F)^c}. Using the fact that the collection of measurable sets is a \sigma-algebra, we can conclude E\cap F is measurable.

Thus F=(E\cap F)\cup (F\setminus E) is the union of two measurable sets and thus is measurable.

Interesting indeed!

 

Math Joke (Fields Arranged by Purity)

Click here for free Career Quiz: https://career-test.com/s/sgamb?reid=210

I came across this joke on another blog: http://phdlife.warwick.ac.uk/

Quite true! A Math student will understand this at the university level and beyond, where Math has no more numbers and is full of symbols and jargon! Although even the most abstract Math has applications, the applications are only discovered years later, hence Pure Math is indeed one of the most pure subjects around.

math joke

Fail H2 Maths Promos or Prelims

For H2 (or H1) Maths students who are getting low marks for internal school exams, do not be overly discouraged. The current trend for schools is to set very tough internal exams (i.e. Promos and Prelims) to spur students to study hard, and (hopefully) ace the eventual final A level exams. If you look at the actual A Level Ten Year Series, you will find that the standard of questions is much easier than Prelim level.

A rule of thumb is that the eventual A level grade is 2 grades above the internal school grade. E.g., in internal exams a student getting D for H2 Maths is most likely equivalent to a B in the final A levels, provided the student continues to study hard.

Jumping from E to A grade has been done by many seniors. Do not give up, continue to believe in yourself, and keep calm while constantly revising.

Do check out this highly condensed H2 Math Notes (comes with free exam papers). The key thing to do before exams is to remember Math formulas (many students forget the AP/GP formulae for instance, and lost some free marks). Constant practice and exposure to questions is also a must.

Here are some sources of true stories:

1) https://www.facebook.com/RJConfessions/posts/220752441406251

To all the J1 and J2 kids who are struggling with math, let me share with you my personal experience. I took H2 math by the way, and refused to drop to H1 when people started dropping.

J1 CT 1: Math: U
J1 promos: Math: S
J2 CT1: Math S
J2 CT2: Math S
J2 Prelims: Math E
A levels: Math A.

The moral of the story is simple: It can be done. My math teacher used to motivate us with stories of seniors who have also flunked their way through math in the 2 years and clinched an A at the end. I didnt really believed it could happen, but I guess I chose to believe it anyways.

2) https://www.reddit.com/r/singapore/comments/3nkq4t/jc_prelims_alevels_correlation/

H2 Math: E A

H2 Chem: D B

H2 Econs: D D

H1 Physics: U A

H1 GP: B A

The grades on the left were prelims and right were my actual results. Of course it depends on your school and how hard they set the prelim papers

Fermat’s Two Squares Theorem (Gaussian Integers approach)

Today we will discuss Fermat’s Two Squares Theorem using the approach of Gaussian Integers, the set of numbers of the form a+bi, where a, b are integers. This theorem is also called Fermat’s Christmas Theorem, presumably because it is proven during Christmas.

Have you ever wondered why 5=1^2+2^2, 13=2^2+3^2 can be expressed as a sum of two squares, while not every prime can be? This is no coincidence, as we will learn from the theorem below.

Theorem: An odd prime p is the sum of two squares, i.e. p=a^2+b^2 where a, b are integers if and only if p\equiv 1 \pmod 4.

(=>) The forward direction is the easier one. Note that a^2\equiv 0\pmod 4 if a is even, and a^2\equiv 1\pmod 4 if a is odd. Similar for b. Hence p=a^2+b^2 can only be congruent to 0, 1 or 2 (mod 4). Since p is odd, this means p\equiv 1\pmod 4.

(<=) Conversely, assume p\equiv 1\pmod 4, where p is a prime. p=4k+1 for some integer k.

First we prove a lemma called Lagrange’s Lemma: If p\equiv 1\pmod 4 is prime, then p\mid (n^2+1) for some integer n.

Proof: By Wilson’s Theorem, (p-1)!=(4k)!\equiv -1\pmod p. (4k)!\equiv [(2k)!]^2\equiv -1\pmod p. We may see this by observing that 4k\equiv p-1\equiv -1\pmod p, 4k-1\equiv -2\pmod p, …, 4k-(2k-1)=2k+1\equiv -2k\pmod p. Thus [(2k)!]^2+1\equiv 0\pmod p and hence p\mid n^2+1, where n=(2k)!.

Then p\mid (n+i)(n-i). However p\nmid (n+i) since p\nmid n=(2k)!. Similarly, p\nmid (n-i). Therefore p is not a Gaussian prime, and it is thus not irreducible.

p=\alpha\beta with N(\alpha)>1 and N(\beta)>1. N(p)=N(\alpha)N(\beta), which means p^2=N(\alpha)N(\beta). Thus we may conclude N(\alpha)=p, N(\beta)=p.

Let \alpha=a+bi. Then p=a^2+b^2 and we are done.

This proof is pretty amazing, and shows the connection between number theory and ring theory.

Abstract Algebra 抽象代数 (石生明教授)

tomcircle's avatarMath Online Tom Circle

这位石教授的”抽象代数”很棒, 一来是他退休前的最后一课, 二来他总结为何老师教不好, 学生上完课好像听到3个大头”鬼” (群group, 环ring, 域field), 但没实际摸过。

他的第一和第二课很好, 与众不同的花时间讲 “动机”: Motivation – Why study Abstract Algebra ?

抽象代数01: Motivation

https://youtu.be/AGd1TZ-IKr0

抽象代数02: 复数扩域 C
$latex
x^{2} +1=0
$

扩域 (Extended Field)数学思维 = 人解决问题的思维
例: 国内不可行的问题, 跳出国门, 扩大到世界领域, 就找到可行的方法。
马云的Alibaba国内不看好, 跑去美国上市, 让他马上成为中国首富的亿万富翁。

View original post

张益唐: 速食店员竟然是数学天才

tomcircle's avatarMath Online Tom Circle

【台湾壹週刊】

速食店员竟然是数学天才

张益唐 (1955 – ) : 北京大学 – 美国数学博士。因为执着数学理论的真理, 得罪美国大学台湾籍论文教授, 毕业后找不到大学教职, 在朋友的 Subway 速食店做会计8年, 潜心业余思考世界数学大难题: Twin Primes Gap, 终于攻破。

他的下一个目标是Riemann Hypothesis, 困扰数学家百年的难题: “素数 (Prime numbers)的分布”都集中在 Zeta function complex plane的 实轴(real = 1/2) 上。大数学家David Hilbert说如果五百年后复活, 第一件事会急着问 “Riemann Hypothesis” 证明了吗?

View original post

James H. Simons,  the mathematician who cracked Wallstreet

tomcircle's avatarMath Online Tom Circle

James H. Simons,  the Jewish mathematician who made $14 billion using Math modelling for Hedge Fund.

[Watch from 31:00 mins to 35 mins].  He told the Nobel Physicist Frank Yang (杨振宁) that the Math “Gauge Theory on Fiber Bundles(纤维丛)” which Yang was developing already existed 30 yrs ago in “Differential Geometry” by SS Chern (陈省身) from Berkeley.

“James H. Simons: Mathematics, Common Sense and Good Luck”

[Video 54:00 mins]
After being billionaire, at old age Simons went back to Math in 2004 to take refuge of sadness of the loss of a son.
He beat the German mathematicians in Differential Co-homology (Topology).

5 Guiding Principles of Success:
1) Don’t run with the pack – be original
2) Choose wonderful partner(s) in research, business…
3) Guided by Beauty
4) Don’t give up !
5) Have good luck.

Jim Simons | TED Talks
“A Rare Interview with the Mathematician Who…

View original post 3 more words

245A, Notes 4: Modes of convergence

Terence Tao's avatarWhat's new

If one has a sequence $latex {x_1, x_2, x_3, ldots in {bf R}}&fg=000000$ of real numbers $latex {x_n}&fg=000000$, it is unambiguous what it means for that sequence to converge to a limit $latex {x in {bf R}}&fg=000000$: it means that for every $latex {epsilon > 0}&fg=000000$, there exists an $latex {N}&fg=000000$ such that $latex {|x_n-x| leq epsilon}&fg=000000$ for all $latex {n > N}&fg=000000$. Similarly for a sequence $latex {z_1, z_2, z_3, ldots in {bf C}}&fg=000000$ of complex numbers $latex {z_n}&fg=000000$ converging to a limit $latex {z in {bf C}}&fg=000000$.

More generally, if one has a sequence $latex {v_1, v_2, v_3, ldots}&fg=000000$ of $latex {d}&fg=000000$-dimensional vectors $latex {v_n}&fg=000000$ in a real vector space $latex {{bf R}^d}&fg=000000$ or complex vector space $latex {{bf C}^d}&fg=000000$, it is also unambiguous what it means for that sequence to converge to a limit $latex {v in {bf R}^d}&fg=000000$ or $latex {v in {bf C}^d}&fg=000000$; it means…

View original post 6,079 more words

mu is countably additive if and only if it satisfies the Axiom of Continuity

Free Career Personality Quiz (Hundreds of people have tried it!)

Let \mu be a finite, non-negative, finitely additive set function on a measurable space (\Omega, \mathcal{A}). Show that \mu is countably additive if and only if it satisfies the Axiom of Continuity: For E_n\in\mathcal{A}, E_n\downarrow\emptyset \implies \mu(E_n)\to 0.

(=>) Assume \mu is countably additive. Let E_n\in\mathcal{A}, E_n\downarrow\emptyset. Then,

\displaystyle \lim_n \mu (E_n)=\mu (\cap_{n=1}^\infty E_n)=\mu (\emptyset).

Suppose \mu(\emptyset)=c. Then \mu(\emptyset)=\mu(\cup_{n=1}^\infty \emptyset)=\sum_{n=1}^\infty c implies c=0.

(<=) Assume \mu satisfies Axiom of Continuity. Let A_n\in\mathcal{A} be mutually disjoint sets. Define E_n=\cup_{i=1}^\infty A_i\setminus \cup_{i=1}^n A_i.

Then E_n\downarrow\emptyset. \lim_n \mu(E_n)=0, \lim_n \mu(\cup_{i=1}^\infty A_i)-\mu (\cup_{i=1}^n A_i)=0. \lim_n \mu(\cup_{i=1}^n A_i)=\mu (\cup_{i=1}^\infty A_i).

Therefore

\begin{aligned}\mu(\cup_{i=1}^\infty A_i)&=\lim_n \mu(\cup_{i=1}^n A_i)\\ &=\lim_n \sum_{i=1}^n \mu (A_i)\\ &=\sum_{i=1}^\infty \mu(A_i) \end{aligned}

Measure that is absolutely continuous with respect to mu

Interesting Career Personality Test (Free): https://mathtuition88.com/free-career-quiz/

Let (X,\mathcal{M},\mu) be a measure space, and let f:X\to [0,\infty] be a measurable function. Define the map \lambda:\mathcal{M}\to[0,\infty], \lambda(E):=\int_X \chi_E f d\mu, where \chi_E denotes the characteristic function of E.

(a) Show that \lambda is a measure and that it is absolutely continuous with respect to \mu.

(b) Show that for any measurable function g:X\to[0,\infty], one has \int_X g d\lambda=\int_X gf d\mu in [0,\infty].

Proof: For part (a), we routinely check that \lambda is indeed a measure.

\lambda(\emptyset)=\int_X \chi_\emptyset f d\mu=\int_X 0 d\mu=0. Let E_i be mutually disjoiint measurable sets.

\begin{aligned} \lambda(\cup_{i=1}^\infty E_i)&=\int_X \chi_{\cup_{i=1}^\infty E_i} f d\mu\\ &=\int_X (\sum_{i=1}^\infty \chi_{E_i}) f d\mu\\ &=\sum_{i=1}^\infty \int_X \chi_{E_i} f d\mu\\ &=\sum_{i=1}^\infty \lambda (E_i) \end{aligned}

If \mu (E)=0, then \chi_{E} f=0 a.e., thus \lambda (E)=0. Therefore \lambda\ll\mu.

(b) We note that when g is a characteristic function, i.e. g=\chi_E,

\begin{aligned} \int_X g d\lambda&=\int_X \chi_E d\lambda\\ &=\lambda (E)\\ &=\int_X \chi_E f d\mu\\ &=\int_X gf d\mu \end{aligned}

Hence the equation holds. By linearity, we can see that the equation holds for all simple functions. Let (\psi_n) be a sequence of simple functions such that \psi_n\uparrow g. Then by the Monotone Convergence Theorem, \lim_{n\to\infty} \int \psi_n d\lambda=\int g d\lambda.

Note that \psi_n f\uparrow gf, thus by MCT, \lim_{n\to\infty}\int\psi_n f d\mu=\int g f d\mu. Note that \int \psi_n d\lambda=\int \psi_n f d\mu. Hence, \int g d\lambda=\int gf d\mu, and we are done.

Calculus: Difficult Integration

tomcircle's avatarMath Online Tom Circle

Question on @Quora:

image

In the French Classe Préparatoire 1st year “Mathematiques Supérieures”,  we wanted to test our admired Math Prof whom we think was a “super know-all” mathematician. We asked him the above question. He immediately scolded us in the unique French mathematics rigor:

“L’intégration n’a pas de sense!
Quelle-est la domaine de définition?”

(The integration has no meaning! What is the domain of definition ?)

He was right! Under the British Math education, we lack the rigor of mathematics. We are skillful in applying many tricks to integrate whatever functions, but it is meaningless without specifying the domain (interval) in which the function is defined ! Bear in mind Integration of a function f (curve) is to calculate the Area under the curve f within an interval (or Domain, D). If f is not defined in D, then it is meaningless to integrate f because there won’t be…

View original post 3 more words

Visual Math

tomcircle's avatarMath Online Tom Circle

image

99% of my friends get it wrong,  except a 13-year-old boy who can ‘see’ it.

Wrong answer : 25

Answer (below):
Try before you scroll down.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

View original post 58 more words

Singapore PSLE 2015 Math

tomcircle's avatarMath Online Tom Circle

image

PSLE is “Primary School Leaving Exams” for 11~12 year-old children sitting at the end of 6-year primary education. The result is used as selection criteria to enter the secondary school of choice.

image

Hint: Without seeing or feeling the weight of the $1 coin, you still can guess the answer. This is the essence of “Singapore Math” — using “Guesstimation“.

Answer (below):
Try before you scroll down.
If wrong answer, please go back to primary school 🙂
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

View original post 118 more words

f integrable implies set where f is infinite is measure zero

Let (X,\mathcal{M},\mu) be a measure space. Let f:X\to [0,\infty] be a measurable function. Suppose that \int_X f d\mu<\infty.

(a) Show that the set \{x\in X:f(x)=\infty\}\subseteq X is of \mu-measure 0. (Intuitively, this is quite obvious, but we need to prove it rigorously.)

(b) Show that the set \{x\in X:f(x)\neq 0\}\subseteq X is \sigma-finite with respect to \mu. i.e. it is a countable union of measurable sets of finite \mu-measure.

We may use Markov’s inequality, which turns out to be very useful in this question.

Proof: (a) Let E_k=\{x\in X:f(x)\geq k\}, where k\in\mathbb{N}. Denote E_\infty=\{x\in X:f(x)=\infty\}.

E_K \downarrow E_\infty, and \mu (E_1)\leq\frac{1}{1}\int_X f d\mu<\infty. (Markov Inequality!)

Then

\begin{aligned}\mu(E_\infty)&=\lim_{k\to\infty}\mu (E_k)\\ &\leq\lim_{k\to\infty}\frac{1}{k}\int f d\mu\ \ \ \text{(Markov Inequality)}\\ &=0 \end{aligned}

Therefore, \mu(E_\infty)=0.

(b) Let S_k=\{x\in X:f(x)\geq\frac{1}{k}\}, k\in\mathbb{N}.

\{x\in X:f(x)\neq 0\}=\cup_{k=1}^\infty S_k

Therefore, \mu(S_k)\leq k\int f d\mu<\infty, and we have expressed the set as a countable union of measurable sets of finite measure.

Once again, do check out the Free Career Quiz!

 

Markov Inequality + PSLE One Dollar Question

Many people have feedback to me that the Career Quiz Personality Test is surprisingly accurate. E.g. people with peaceful personality ended up as Harmonizer, those who are business-minded ended up as Entrepreneur. Do give it a try at https://mathtuition88.com/free-career-quiz/. Please help to do, thanks a lot!

Also, some recent news regarding PSLE Maths is that a certain question involving weight of $1 coins appeared. It is very interesting, and really tests the common sense and logical thinking skills of kids.

Markov inequality is a useful inequality that gives a rough upper bound of the measure of a set in terms of an integral. The precise statement is: Let f be a nonnegative measurable function on \Omega. The Markov inequality states that for all K>0, \displaystyle \mu\{x\in\Omega:f(x)\geq K\}\leq\frac{1}{K}\int fd\mu.

The proof is rather neat and short. Let E_K:=\{x\in\Omega: f(x)\geq K\} Then,

\begin{aligned} \int f d\mu &\geq \int_{E_K} fd\mu\\ &\geq \int_{E_K}K d\mu\\ &=K \mu(E_K) \end{aligned}

Therefore, \mu(E_K)\leq\frac{1}{K}\int fd\mu.

Free Career Personality Quiz (Please help to do!)

Facebook Profile Picture 03

URL: https://career-test.com/s/sgamb?reid=210

The results of this Personality Test is quite surprisingly accurate, do give it a try to see if you are a Careerist, Entrepreneur, Harmonizer, Idealist, Hunter, Internationalist or Leader?

Do try out this Free Career Guidance Personality Test at https://career-test.com/s/sgamb?reid=210 while it is still available!

Benefits of doing the (Free) Career Test:

  • Get familiar with the top companies in Singapore
  • There are seven distinct career types based on career preferences, goals and personality. Get to know yours! (My result: Harmonizer)
  • Take part in the annual Universum survey and win prizes!

Necessary and Sufficient Condition for Integrability in finite measure space

Facebook Profile Picture 03

URL: https://career-test.com/s/sgamb?reid=210

The results of this Personality Test is quite surprisingly accurate, do give it a try to see if you are a Careerist, Entrepreneur, Harmonizer, Idealist, Hunter, Internationalist or Leader?

Do try out this Free Career Guidance Personality Test at https://career-test.com/s/sgamb?reid=210 while it is still available!

Benefits of doing the (Free) Career Test:

  • Get familiar with the top companies in Singapore
  • There are seven distinct career types based on career preferences, goals and personality. Get to know yours! (My result: Harmonizer)
  • Take part in the annual Universum survey and win prizes!

Let (\Omega, \Sigma, \mu) be a finite measure space. Suppose that f\geq 0 is a measurable function on \Omega. Let E_n:=\{\omega\in\Omega:f(\omega)\geq n\} for each n\in \mathbb{N}\cup\{0\}. Show that f is integrable if and only if \sum_{n=0}^\infty \mu(E_n)<\infty.

This proof has a cute solution that is potentially very short. We will elaborate more on this proof. Other approaches include using Markov’s Inequality / Chebyshev’s inequality.

Proof: Consider g=\sum_{n=1}^\infty I_{E_n}.

Note that for each n\geq 0, n\in\mathbb{N} on E_n\setminus E_{n+1}, g=n, while n\leq f<n+1. Therefore g\leq f<g+1 on \Omega.

Integrating with respect to \mu, we get \int_{\Omega} gd\mu\leq\int_{\Omega} fd\mu<\int_{\Omega} g+1d\mu.

\displaystyle\boxed{\sum_{n=1}^\infty \mu (E_n)\leq \int_\Omega f d\mu<\sum_{n=1}^\infty\mu(E_n)+\mu(\Omega)}

(=>) Now assuming f is integrable, i.e. \int fd\mu<\infty, we have \sum_{n=1}^\infty \mu(E_n)<\infty. \mu(E_0)=\mu(\Omega)<\infty. Therefore \sum_{n=0}^\infty\mu(E_n)<\infty.

(<=) Conversely, if \sum_{n=0}^\infty\mu(E_n)=\sum_{n=1}^\infty \mu(E_n)+\mu(\Omega)<\infty, then \int_\Omega f d\mu<\infty.

We are done.

Note: For a more rigorous proof of \int gd\mu=\sum_{n=1}^\infty \mu (E_n) we can use MCT (Monotone Convergence Theorem).

Let g_k=\sum_{n=1}^k I_{E_n}. Then g_k\uparrow g. By MCT, \int gd\mu=\lim_{k\to\infty} \int g_k d\mu=\lim_{k\to\infty} \sum_{n=1}^k \mu (E_n)=\sum_{n=1}^\infty \mu(E_n).

εδ Confusion in Limit & Continuity

tomcircle's avatarMath Online Tom Circle

1. Basic:
|y|= 0 or > 0 for all y

2. Limit: $latex displaystylelim_{xto a}f(x) = L$ ; x≠a
|x-a|≠0 and always >0
hence
$latex displaystylelim_{xto a}f(x) = L$
$latex iff $
For all ε >0, there exists δ >0 such that
$latex boxed{0<|x-a|<delta}$
$latex implies |f(x)-L|< epsilon$

3. Continuity: f(x) continuous at x=a
Case x=a: |x-a|=0
=> |f(a)-f(a)|= 0 <ε (automatically)
So by default we can remove (x=a) case.

Also from 1) it is understood: |x-a|>0
Hence suffice to write only:
$latex |x-a|<delta$

f(x) is continuous at point x = a
$latex iff $
For all ε >0, there exists δ >0 such that
$latex boxed{|x-a|<delta}$
$latex implies |f(x)-f(a)|< epsilon$

View original post

Newtonian Calculus not rigorous !

tomcircle's avatarMath Online Tom Circle

Why Newton’s Calculus Not Rigorous?

$latex f(x ) = frac {x(x^2+ 5)} { x}$ …[1]

cancel x (≠0)from upper and below => $latex f(x )=x^2 +5 $

$latex mathop {lim }limits_{x to 0} f(x) =x^2 +5= L=5 $ …[2]

In [1]: we assume x ≠ 0, so cancel upper & lower x
But In [2]: assume x=0 to get L=5
[1] (x ≠ 0) contradicts with [2] (x =…)

This is the weakness of Newtonian Calculus, made rigorous later by Cauchy’s ε-δ ‘Analysis’.

View original post 1 more word

Rigorous Calculus: ε-δ Analysis

tomcircle's avatarMath Online Tom Circle

Rigorous Analysis epsilon-delta (ε-δ)
Cauchy gave epsilon-delta the rigor to Analysis, Weierstrass ‘arithmatized‘ it to become the standard language of modern analysis.

1) Limit was first defined by Cauchy in “Analyse Algébrique” (1821)

2) Cauchy repeatedly used ‘Limit’ in the book Chapter 3 “Résumé des Leçons sur le Calcul infinitésimal” (1823) for ‘derivative’ of f as the limit of

$latex frac{f(x+i)-f(x)}{i}$  when i ->…

3) He introduced ε-δ in Chapter 7 to prove ‘Mean Value Theorem‘: Denote by (ε , δ) 2 small numbers, such that 0< i ≤ δ , and for all x between (x+i) and x,

f ‘(x)- ε < $latex frac{f(x+i)-f(x)}{i}$ < f'(x)+ ε

4) These ε-δ Cauchy’s proof method became the standard definition of Limit of Function in Analysis.

5) They are notorious for causing widespread discomfort among future math students. In fact, when it…

View original post 92 more words

German Terms

German before WW2 was the World’center of Science (Einstein etc) and Modern Math (Gauss, Klein, Hilbert etc), that’s why we inherit some letter symbols eg. Z (Zahl, Integer) …

tomcircle's avatarMath Online Tom Circle

1. The electron orbits: first 4 orbits from atom

s, p, d, f
s = Sharfe (Sharp)
p =prinzipielle (principle)
d = diffusiv (diffuse)
f= fundamentale (fundamental)
2. eigen (special)
eigenvector
eigenvalue
eigenfunction
eigenfrequency
3. Math:
e = neutral element (I=Identity)
K=Korps (Fields)
Z = Zahl (Integer)
4. Physics:
F-center = Color Center  (F=Farbe=color)
Umklapp process = reverse process
Aufbau principle (quantum chemistry) = Building (bau) Up (Auf)  principle

View original post

Abstract Math discomforts

Abstract Algebra is the killer Math subject for university-bound Singaporean A-level students educated in the British GCE syllabus. Except a fews who are born with the gift, most of them get lost in the first year of university. Yet Abstract Algebra is important math “language” of science and technology : IT, Chemistry, Physics, Advanced Math… if you want to describe a complex structure (quantum physics, crystallography), algorithm (search), method (encryption), you use this precise and concise language “Abstract Algebra” (such as Group, Vector Space, …). Countries like China and USA havevmade Abstract Algebra a compulsory subject for 1st year undergrads in Science, Engineering, IT students beside Math majors …

tomcircle's avatarMath Online Tom Circle

3 Wide Discomforts For Abstract Math Students

1. Group : Coset, Quotient group, morphism…
2. Limit ε-δ: Cauchy
3. Bourbaki Sets: Function f: A-> B is subset of Cartesian Product AxB.

Students should learn from their historical genesis rather than the formal abstract definitions

<a href=”http://http://en.wikipedia.org/wiki/Wu_Wenjun“>Wu Wenjun (吳文俊) on Learning Abstract Math

“…It is more important to understand the ‘Principles’ 原理 behind, à la Physics (eg. Newton’s 3 Laws of Motion), and not blinded by its abstract ‘Axioms’ 公理.”

Prof I.Herstein http://en.wikipedia.org/wiki/Israel_Nathan_Herstein

“… Seeing Abstract Math for the first time, there seems to be a common feeling of being adrift, of not having something solid to hang on to.”

“Do not be discouraged. Stick with it! The best road is to look at examples. Try to understand what a given concept says, most importantly, look at particular, concrete examples of the concept.”

“

View original post 47 more words

Probability by 2 Great Friends

tomcircle's avatarMath Online Tom Circle

Today Probability is a “money” Math, used in Actuarial Science, Derivatives (Options) in Black-Scholes Formula.

In the beginning it was “A Priori” Probability by Pascal (1623-1662), then Fermat (1601-1665) invented today’s “A Posteriori” Probability.

“A Priori” assumes every thing is naturally “like that”: eg. Each coin has 1/2 chance for head, 1/2 for tail. Each dice has 1/6 equal chance for each face (1-6).

“A Posteriori” by Fermat, then later the exile Protestant French mathematician De Moivre (who discovered Normal Distribution), is based on observation of “already happened” statistic data.

Cardano (1501-1576) born 150 years earlier than Pascal and Fermat, himself a weird genius in Medicine, Math and an addictive gambler, found the rule of + and x for chances (he did not know the name ‘Probability’ then ):

Addition + Rule: throw a dice, chance to get a “1 and 2” faces:
1/6 +1/6 = 2/6 = 1/3

View original post 193 more words

Galois Theory Simplified

tomcircle's avatarMath Online Tom Circle

Galois discovered Quintic Equation has no radical (expressed with +,-,*,/, nth root) solutions, but his new Math “Group Theory” also explains:
$latex x^{5} – 1 = 0 text { has radical solution}$
but
$latex x^{5} -x -1 = 0 text{ has no radical solution}$

Why ?

$latex x^{5} – 1 = 0 text { has 5 solutions: } displaystyle x = e^{frac{ikpi}{5}}$
$latex text{where k } in {0,1,2,3,4}$
which can be expressed in
$latex x= cos frac{kpi}{5} + i.sin frac{kpi}{5} $
hence in {+,-,*,/, √ }
ie
$latex x_0 = e^{frac{i.0pi}{5}}=1$
$latex x_1 = e^{frac{ipi}{5}}$
$latex x_2 = e^{frac{2ipi}{5}}$
$latex x_3 = e^{frac{3ipi}{5}}$
$latex x_4 = e^{frac{4ipi}{5}}$
$latex x_5 = e^{frac{5ipi}{5}}=1=x_0$

=>
$latex text {Permutation of solutions }{x_j} text { forms a Cyclic Group: }
{x_0,x_1,x_2,x_3,x_4} $

Theorem: All Cyclic Groups are Solvable
=>
$latex x^{5} -1 = 0 text { has radical solutions.}$

However,
$latex x^{5} -x -1 =…

View original post 41 more words

Interesting Analysis Question (Measure Theory)

Do try out this Free Career Guidance Personality Test at https://career-test.com/s/sgamb?reid=210 while it is still available!

Benefits of doing the (Free) Career Test:

  • Get familiar with the top companies in Singapore
  • There are seven distinct career types based on career preferences, goals and personality. Get to know yours! (My result: Harmonizer)
  • Take part in the annual Universum survey and win prizes!

Let f\geq 0 be a measurable function with \int f d\mu<\infty. Show that for any \epsilon>0, there exists a \delta(\epsilon)>0 such that for any measurable set E\in\mathcal{A} with \mu(E)<\delta(\epsilon), we have \int_E f d\mu<\epsilon.

Proof: For M>0, we define f_M(x)=\min (f(x),M)\leq M, for all x\in \Omega.

Then f=f_M+(f-f_M).

Let \delta=\epsilon/2M. Then for any E\in\mathcal{A} with \mu(E)<\delta,

\begin{aligned}\int_E f_M d\mu &\leq \int_E M d\mu\\ &=\mu (E)M\\ &<\delta M\\ &=(\epsilon/2M)M\\ &=\epsilon/2 \end{aligned}

Note that f_M\uparrow f. By Monotone Convergence Theorem,

\int f d\mu=\lim_{M\to\infty}\int f_M d\mu.

Therefore \lim_{M\to\infty}\int f-f_M d\mu=0.

We can choose M sufficiently large such that

\int_E f-f_M d\mu \leq \int f-f_M d\mu <\epsilon/2.

Then

\begin{aligned} \int_E f d\mu&=\int_E f_M d\mu+\int_E f-f_M d\mu\\ &<\epsilon/2+\epsilon/2\\ &=\epsilon \end{aligned}

We are done!

 

The Arrival of New Era of “Knowledge Sharing”

tomcircle's avatarMath Online Tom Circle

2010 Steve Jobs declared Post-PC era has arrived with iPhone/iPad,  little did he know that he had accidentally also brought the Post-TV & Post-Publication (books, Newspapers) on iPhone/iPad platform for YouTube, ebooks.
Today,  you don’t have to sit on sofa at scheduled time to watch TV programmes,  buy/loan/housekeep books, subscribe to political-biased  newspapers.

The advent of Web 2.0 and Internet of Things (IoT) will open up the new era of freedom of “Knowledge Sharing”:
1. Instead of reading 100 books to understand a complex economic/politics/history/science topic, you can go YouTube to attend free seminars by TED, MOOC (Cousera, Khan Academy…), or follow YouTube series by book expert reviewers (罗辑思维, 袁腾飞, 百家论坛, 宋鸿兵货币战争)…
2. You can ask any questions on “Quora”. Anybody with the expertise will volunteer to teach you.
3. You can keep your reading notes in text, video and hyperlink to the vast internet resources (wikipedia, ..) and shared…

View original post 9 more words

A solvable group that has a composition series is necessarily finite

Facebook Profile Picture 03

Do try out this Free Career Guidance Personality Test at https://career-test.com/s/sgamb?reid=210 while it is still available!

Benefits of doing the (Free) Career Test:

  • Get familiar with the top companies in Singapore
  • There are seven distinct career types based on career preferences, goals and personality. Get to know yours! (My result: Harmonizer)
  • Take part in the annual Universum survey and win prizes!

Let G be a solvable group. We prove that if G has a composition series, then G has to be finite. (Note that this is sort of a converse to “A finite group has a composition series.”)

Let G=G_0\geq G_1\geq \dots\geq G_n=1 be a composition series of G, where each factor G_i/G_{i+1} is simple.

Since G_i and G_{i+1} are solvable (every subgroup of a solvable group is solvable), the quotient G_i/G_{i+1} is also solvable.

We can prove that G_i/G_{i+1} is abelian. Since (G_i/G_{i+1})'\trianglelefteq G_i/G_{i+1}, by the fact that the factor is simple, we have (G_i/G_{i+1})'=1 or G_i/G_{i+1}.

If (G_i/G_{i+1})'=G_i/G_{i+1}, then this contradicts the fact that G_i/G_{i+1} is solvable. Thus (G_i/G_{i+1})'=1 and G_i/G_{i+1} is abelian.

Key step: G_i/G_{i+1} is simple and abelian, G_i/G_{i+1}\cong\mathbb{Z}_{p_i} for some prime p_i.

Since |G_{n-1}|=p_{n-1}, so we have that |G_{n-2}|=|G_{n-2}/G_{n-1}||G_{n-1}|=p_{n-2}p_{n-1}. By induction, |G_i|=p_i p_{i+1}\dots p_{n-1}.

|G|=|G_0|=p_0p_1\dots p_{n-1}. Thus G is finite.

 

Conjugacy Classes of non-abelian group of order p^3

Do try out this Free Career Guidance Personality Test at https://career-test.com/s/sgamb?reid=210 while it is still available!

Benefits of doing the (Free) Career Test:

  • Get familiar with the top companies in Singapore
  • There are seven distinct career types based on career preferences, goals and personality. Get to know yours! (My result: Harmonizer)
  • Take part in the annual Universum survey and win prizes!

Let p be a prime, and let G be a non-abelian group of order p^3. We want to find the number of conjugacy classes of G.

First we prove a lemma: Z(G) has order p.

Proof: We know that since G is a non-trivial p-group, then Z(G)\neq 1. Since Z(G)\trianglelefteq G, by Lagrange’s Theorem, |Z(G)|=p,p^2,\text{or }p^3.

Case 1) |Z(G)|=p. We are done.

Case 2) |Z(G)|=p^2. Then |G/Z(G)|=p^3/p=p. Thus G/Z(G) is cyclic which implies that G is abelian. (contradiction).

Case 3) |Z(G)|=p^3. This means that the entire group G is abelian. (contradiction).

Next, let O(x_1),\dots, O(x_n) be the distinct conjugacy classes of G.

O(x_i)=\{gx_i g^{-1}:g\in G\}, where C_G(x_i)=\{g\in G:gx_i=x_ig\}.

Then by the Class Equation, we have \displaystyle p^3=|G|=\sum_{i=1}^n [G:C_G(x_i)].

If x_i\in Z(G), then C_G(x_i)=G, which means [G:C_G(x_i)]=1.

If x_i \notin Z(G), then C_G(x_i)\neq G. Since x_i\in C_G(x_i), thus Z(G)\subsetneq C_G(x_i). Thus we have p=|Z(G)|<|C_G(x_i)|<|G|=p^3. Since C_G(x_i) is a subgroup of G, Lagrange’s Theorem forces |C_G(x_i)|=p^2. Thus [G:C_G(x_i)]=p^3/p^2=p.

By the Class Equation, we thus have p^3=p+(n-p)p, which leads us to \boxed{n=p^2+p-1}.