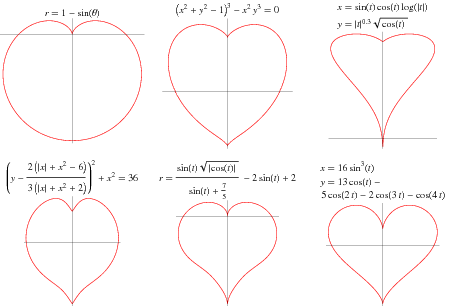Category: Uncategorized
Heron’s Formula
Introduction to Apollonian circle packings (tangent)
This is not my area of research at all, but I think it’s super cool. The first time I heard of Apollonian circle packings was at that conference I went to in Marseille last month, during the first lecture of Hee Oh’s minicourse. So here’s a quick write up background of the first third of that lecture.
These packings and all this theory come from one dude, Apollonius of Perga, who wrote a bunch of math books back around 200 BC. Literally this math has been around for 2200 years. Here’s a paper submitted a month ago which is a generalization of Apollonius’s problem from circles to spheres. Math is so amazing! We live in history!
To understand the problem, we’ll have to do a quick geometry brush up. We say that two shapes or curves or lines in the plane are tangent if they touch at exactly…
View original post 1,181 more words
Is Google Making You More Forgetful? [Infographic]
张益唐在伯克利的演讲絮记 (转载)
 张的主要结果是一流的,他证明了关于素数分布的一个里程碑式的定理。 — 美国数学年鉴审稿人,2013年5月
基本上,这个领域里没有人知道他(张益唐),而现在,仿似一夜之间,他证明了一个可以名列数论历史上最伟大结果之一的定理。这个领域内的世界顶级专家已经竭尽全力的使用这类方法去解决这个大问题,而他并非一个知名专家,却在所有专家倒下的地方成功的站了起来。 — Adrew Granville 【Note】本文作者的数学修养和知识都极其有限,对于数学专业的人来说,基本上是数学盲。因此本文只属于絮记 —- 从一个非数学专业的业余爱好者的角度描写旁听张老师在伯克利演讲的部分过程,并附带一些小花絮。行文中如有幼稚之处请谅解,还有期待专业报道或评论的人士请出门左拐并客气一些,谢谢。 by 灵致 如果评选本年度最值得华人世界为之骄傲的事,张益唐奇迹般的崛起绝对是其中一个,至少在我眼里是如此。 无论时光过去多少年,当我们都老去,离开了这个世界,张先生的故事都将流传下去,直到最后的最后。
 就在两天前,我突然收到系里一个同学的邮件,令我惊讶的提到张益唐先生将于本周四的下午在伯克利演讲他在素数有界距离方面的最新工作。 从今年的五月份开始, 我在美国媒体以及周围的社交网络的各种报道开始爆炸式发展的时候开始,就和很多人一样密切关注张先生的各种消息,分析以及评价。那个时候,曾经一度冷清的MITBBS数学版罕见式的大爆发,持续数月的讨论张的结果。虽然大部分都是八卦类的,但是大家对于数学的热情似乎一下子被那么一簇火点燃了。
 张的文章很快就在网上可以下载,虽然我完全不懂,但觉得非常厉害,于是很崇敬的下载下来,读了最前面3页。然后的然后,在符号介绍完毕进入证明技术细节的时候,我就lost了。但是网友写的证明总结和评论,以及陶哲轩的blog文章,我都看了,所以在大的picture上知道他大概是如何做到的,然后是如何的不易。 这一次,我居然有机会去听一听— 哪怕一窍不通,但张老师的学问和人品也足以让我放下手头的一切去旁听一下。 应该说,我是满怀期待并内心很激动的。
 可是昨天才发现演讲的时间和我们组会时间冲突,然后接到导师的邮件,说本来准备来我们组会给talk的人困在洛杉矶无法如期到达,于是导师问我可不可以由我来讲点自己暑假做的东西。 我当时觉得很遗憾,但是还是硬着头皮答应了。不过,我想到一个点子— 因为组会时间和张的演讲时间只有半个小时交集,我可以压缩我的talk时间,然后说不定组会提前结束,我可以赶过去。 结果是,因为有教授过来访问并参加了组会,加上大家讨论很积极,原本我计划好一个小时速战速决的talk足足用了一个半小时。而且我讲的中间,google calendar还跳出来提醒说“Yitang Zhang 给talk 啦!”, 众人都笑了。等我急匆匆的放好东西赶到Evans的60号教室时,居然里面在上课— 放着二战的电影。正在我一头黑线不明其里的时候,门口有人告诉我talk改在了4点钟开始。我当时高兴极了,想着总算没有错过。 那个教室很快下课,学生鱼贯而出。 我在前面找了个不错的位置,在余下的四十分钟时间里静静的等待。 突然,旁边有人叫道,哇,那就是他!
 我抬头,几个数学系的老教授和一个白衬衫黑西装裤打扮的中国人聊得火热。那个中国人,就是张老师了。 旁边似乎是媒体的人架着摄像头在跟拍。几个设备支持人员围着他,帮他带上麦克风等设备。 因为这边有所谓的伯克利时间的传统(可以比规定的时间迟到10分钟),那会儿人还不多。张老师一边走,一边看了一眼我们几个人,正好看到我的时候,我脑子一抽经,脱口就甩出一句中文:“张老师好!”, 他双手摆摆,说“你好你好!”。
 不一会儿,talk快开始了,人越来越多,空位置越来越少。我看到很多平常不经常出现的老教授也陆续赶来。 在主持人简短的介绍完毕之后,全场热烈鼓掌表示欢迎。张老师双手微微张开持续向大家挥手致谢。 之后,他就开口讲话了。 说实在的,他的口语是比较重的中式口音,我们听起来毫无问题,但是估计有一些美国人会被虐得不行。
 他开始就说要讲的内容是素数分布算术数列的最新进展。 然后就掠起袖子拿起粉笔开始在黑板上写divisor function和von Mangoldt function等,并由此开始定义Delta函数,以及后面的广义黎曼猜想和他的结果和思路。从开始到最后持续了四十五分钟左右,他一路讲得很顺畅。尽管不懂,但我认真记笔记。其中一些数学的技术细节,因为我数学水平不够,无法做出好的评论。他的talk,总共用了8快黑板,我抄了3页笔记。
 其中有一次他电话响,他连声道歉并把电池拔了下来(那种很老式的翻盖手机),大家宽容的笑。 直到讲到最后,他面向观众,说由此,我们可以证明素数距离有界。全场再次爆发以热烈的掌声,持续很长时间—- 这可以看出大家对他是很尊敬的。
 接下来是问题时间,却突然全场冷场,没有人提问。我们都环顾四周,不知道为何那些数学大牛不趁机提点问题,气氛似乎一下子紧张了一些。我这个时候脑子又抽经了,举了手,张老师注意到我,然后主持人示意我可以提问。 我当时知道很多人在看我,也知道我有可能很丢脸,但似乎在这种时候我犯二的精神总能让我无所畏惧。我吸了一口气,说我要问一个很幼稚的问题。他点头示意。我就说,我注意到你的证明中有一个参数用了一个数 1/2 + 1/584, 以及有个重要的步骤约束条件用的是d小于x的1/1168次方,我不知道为什么你会特别的选择这些数字(比如584和1168而非其他),而不是其他数字。尽管我的本意是说我理解证明了这些特例,就证明了最后的结果,但是对于选择这些数字,显然不是任意的,肯定需要满足某种特别的性质或者其他动机而不是随手挑一个就可以的,否则他肯定会选择符合条件的比较优美自然一点的数字。 他最后解释说是因为他自己简单的验算,这些数字正好符合要求而且他那时候太累了,就直接用了。
 后来气氛活跃了一些,有个老教授问他用计算机算的么。他用手在空中画了一个小方框,说我用普通的计算器算的。全场大笑。 在另外一个明显很懂的教授问了一个技术问题后,没有人问题了,演讲就此结束。人们开始陆续离开,我反正之后也没有啥事,就坐着没动。 张老师很恭敬的向坐在前排的一个老教授致意,然后似乎想和他讨论其中一个技术问题,那个老教授起身去和他讨论。旁边的一个似乎是媒体的工作人员觉得这镜头不错,立马跑上去跟拍他们讨论的过程。张老师很大气的讲着,丝毫没有看镜头和受到干扰。
 最后教室里只剩下几个人的时候,他又掠起袖子,在离开之前想把擦黑板檫干净。这点很令人感动。中间几次有人打断他檫黑板和他聊两句,他很礼貌的停下来和别人说话,之后接着檫,直到最后一块的时候,有个老教授说你不用檫了,留着挺好,他才停下来。 不一会儿,他接到一个电话,是他太太打过来的。他立马变成了中文模式,普通话甩得可标准了。那时他看到坐在座位上翻笔记的我,示意性的笑了笑。  我起身离开的时候,正好在出门的时候遇到他。我问他之后要去干嘛,他说他太太过来接他,要在一个灯塔下面见面。 我内心想笑,因为这是我第一次听到有人把伯克利的钟塔叫灯塔,感觉像海边的信号塔似的。 一边正要出门,我说,你说的是不是校园中心的那个塔? 他说是啊是啊,就是那个灯塔。 我出了教室门左拐,看他往右拐,似乎迷惑住了不知道往何处走。Evans hall的结构是比较不容易摸清方向。 我就问他是不是不知道往哪里走?他很憨厚的笑了笑点着头。 我就说要不我带你过去把,走近道几步就到了。他连声说谢谢。 走的路上,我问他是不是讲的很累,他说很okay啊,这算很轻松的了。 然后我就说我也下了你的论文,可惜我啥都不懂,但我觉得你开头两页写的真好,连我这种一窍不通的人都读懂了。 他就看着我笑,然后顿了顿,说其实啊,我很用心的写的,但是第五页写的最用心,因为那一页如果写不清楚,很多人会觉得你是胡闹。最后也是写好了那小部分,才觉得一切就很明了。
 他还说,他在投稿前两个月的时间里累得精疲力尽,但是自我检查是必不可少的。最后,当他通过各种角度去验证都没有发现证明的错误的时候,就松了一口气,放心的投了出去。 我和他开玩笑说这听起来就好比是多次随机采样,反复验证直到你确定正确的置信度达到了95%以上才放手。他又笑。 期间我们谈到他太太,可以透露的内容是,他太太在Mountain View工作,从事的工作不是大家一致猜测的程序员,而是一个我个人觉得很不错的工作(尽管他用比较搞笑的语言描述的)。而且,在我看他讲他太太的神情和语气可以看出,他们的感情很好。 我把他带到萨瑟塔(Sather Tower)下面朝向金门大桥的地方,站了一会儿也没有看到他太太的人。 我就提议他给太太打电话,然后等她过来。
之后,我和他告别,就离开了。 其实,他并不知道我的名字。但我想他应该知道,有很多人,包括我,是很敬佩他的。 有很多人关心他能不能继续做出世界顶级的工作,比如攻克广义黎曼猜想等等,也有很多人质疑和辩论他是否够格称作大师, 所谓排名几何或者和陶哲轩比谁更牛等。但是我,相信和不少人一样,只是希望他未来能够过得更开心和幸福。其他的,不那么重要了。
 灵致 2013年9月12日 加州·湾区 附事件概要 时间:2013年9月12日 地点:Evans Hall, Room 60. 主讲:张益唐 听众:数学系教授和学生,还有一半啥都不懂只为瞻仰而去的听众,比如我。 |
Dissecting The Riemann Zeta Function
 The Riemann Zeta function is an extremely important special function of mathematics and physics. It is intimately related with very deep results surrounding the prime numbers. Now why would we want to care about prime numbers? Well, the entire concept of web security is built around prime numbers. Most of the algorithms for banking security, cryptography, networking, communication, etc are constructed using these prime numbers and the related theorems. The reason we do this is because of the inherently sporadic nature of prime numbers. You never know where the next one is going to appear on the number line! So what does that have to do with the Reimann zeta function? If prime numbers are random, what’s the point of looking into them?
The Riemann Zeta function is an extremely important special function of mathematics and physics. It is intimately related with very deep results surrounding the prime numbers. Now why would we want to care about prime numbers? Well, the entire concept of web security is built around prime numbers. Most of the algorithms for banking security, cryptography, networking, communication, etc are constructed using these prime numbers and the related theorems. The reason we do this is because of the inherently sporadic nature of prime numbers. You never know where the next one is going to appear on the number line! So what does that have to do with the Reimann zeta function? If prime numbers are random, what’s the point of looking into them?
View original post 1,248 more words
Dyscalculia
Free Mathematics Books Online
Check out this amazing website: http://www.sciencebooksonline.info/mathematics.html
It has many free mathematics books online for self study! (More of university level material)
MM4B Quadratic Functions
MM4B Quadratic Functions. This video re-visits Quadratic Functions, presents a summary of the features of Quadratic Functions, shows the various ways of solving quadratic equations, talks about the use of the discriminant and then show how completing the square can be used to describe the transformation steps from the basic function of a quadratic to a new variant in turning point form. The video was made for students studying Mathematical Methods (CAS) in Year 12, a course fully prescribed by the Victorian Curriculum and Assessment Authority in the State of Victoria, Australia
Rate of Change
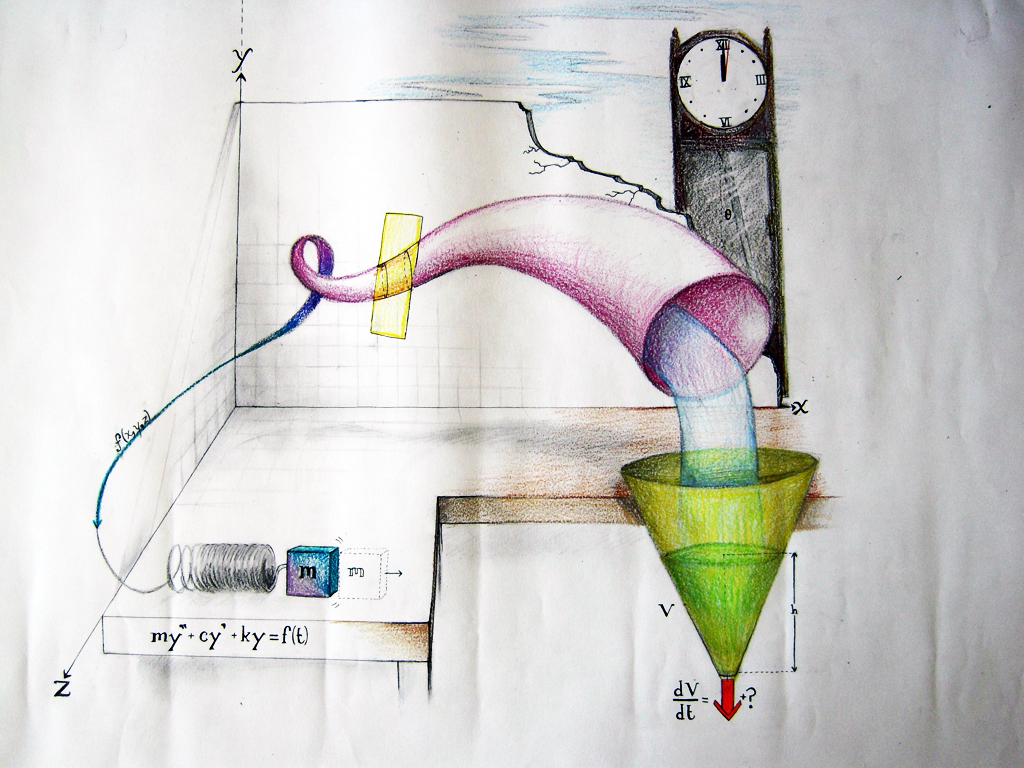
HMC Interface Compendium of Student Work
This colored pencil drawing was created by Elly Schofield in Spring 2010 for an introductory course in Differential Equations. The goal of the work is to visually represent the shared context and commonalities of applications of ordinary differential equations. Its delicate surrealism displays multiple applications with a striking precision, juxtaposing full color and grayscale renditions of the flow rate of a fluid, a mass-spring system, and a pendulum.
Wordads Review
How to make money online using WordPress
There are currently only three options for advertising on WordPress.com:
1) No Ads Option
2) The default free option
3) Wordads
(Source: http://wordads.co/faq/)
For those who have a custom WordPress.com domain, you can apply to Wordads, and Wordpress can run ads on all of your pages and you share in the income. (http://wordads.co/signup/)
Review: Wordads vs Adsense
AdSense isn’t an option on WordPress.com, so currently bloggers on WordPress.com have to use Wordads.
Some review online regarding the payment option of Wordads and Wordads earnings include:
One thing good (or bad) about Wordads is that it is impression based, clicking on ads is not required. This may be good since usually not many people click on ads. On the other hand, impression based ads tend to have lower pay rates.
Wordads Tips
Be sure to select a Wordads-friendly theme. (I am using the Coraline Theme) This enables you to select the option “Show additional ad units” which would show additional ad units on your blog. This could potentially triple your ad impressions.
Any comments about Wordads? Feel free to drop a comment below!
Why All Currencies Use Only 4 Numbers (1, 2, 5, 10)?
All currency coins or notes are issued in these 4 denominations: {1, 2, 5, 10} but not {3, 4, 6, 7, 8, 9}.
Reason: These 4 numbers {1, 2, 5, 10} just need at most 2 operations (+ or -) to generate any number from 1 to 10.
(1 = 1)
(2 = 2)
3 = 1 + 2
4 = 2 +2
(5 = 5)
6 = 1 + 5
7 = 2 + 5
8 = 10 – 2 = 1 + 2 + 5
9 = 10 – 1 = 2 + 2 + 5
(10 = 10)
Why is math research important?
As I’ve already described, I’m worried about the oncoming MOOC revolution and its effect on math research. To say it plainly, I think there will be major cuts in professional math jobs starting very soon, and I’ve even started to discourage young people from their plans to become math professors.
I’d like to start up a conversation – with the public, but starting in the mathematical community – about mathematics research funding and why it’s important.
I’d like to argue for math research as a public good which deserves to be publicly funded. But although I’m sure that we need to make that case, the more I think about it the less sure I am how to make that case. I’d like your help.
So remember, we’re making the case that continuing math research is a good idea for our society, and we should put up some money towards it…
View original post 767 more words
Happy Valentine’s Day
Mathematics, Learning and Technology
 Click on the image and move that slider!
Click on the image and move that slider!
In what happily seems to have become an annual tradition Desmos have provided you with the means to send a math-o-gramto the mathematicians in your life!
This year you can even use the Desmos API …
Elsewhere – express your feelings for WolframAlpha!
and here’s a logic starter from Transum for Valentine’s Day!
Wishing Mathematicians everywhere a happy day and if you are a UK teacher about to start half term – have a lovely week!
Base Number Conversions
SM3C Inverse Circular Functions
SM3C Inverse Circular Functions. Inverse Circular Functions of Cosecant, Secant and Cotangent are introduced and then transformations of the their graphs are explored and implied domains and ranges are calculated. The video was produced for students undertaking Specialist Mathematics in Year 12 in the State of Victoria, Australia.
Oxford and Cambridge application for Singaporean students
Oxbridge admissions for Singaporean applicants

Hello reader,
I am an applicant to Oxford/Cambridge, and sometime after I was informed about whether I was accepted/rejected, I decided to write up on the application process for new applicants who may not know too much about Oxford and Cambridge. I have recently done some research, whipped up some numbers which I hope can help you in your application. Most people start off thinking about applying to Oxford and Cambridge (and other famous universities) without anything except their ambition to start with, and I hope this guide can provide you with useful information for your university applications.
This is written mostly from a Singaporean student’s perspective, although some information is applicable to applicants from other countries as well.
Overview of Oxford and Cambridge
Oxford and Cambridge are the oldest and 2nd oldest universities in the English speaking world respectively, and 2nd and 3rd oldest in the world…
View original post 5,931 more words
freeexampapers
Check out our site on freeexampapers:
Infinity Series I: Finite Area with Infinite Perimeter
| This is the first entry of the “Infinity Series”, which will introduce you to the peculiar world of infinity. Today, we will be talking about something with finite area but with infinite perimeter. That sounds odd and impossible but I’ll show you how it can be done. |
Draw a circle and an equilateral triangle inside it, with the three vertices of the triangle touching the circle.

Since we know that the circle has a finite area, the triangle inside must have finite area as well. At this point, we still have finite perimeter on the triangle as well.
Now, divide each edge of the triangle into thirds; draw an equilateral triangle using the middle piece of the divided edges as the base, as follows:

With careful observation, you can see that the perimeter has increased. Specifically, the perimeter increased by a third: instead of one…
View original post 301 more words
7 Equations to Show Valentine Passion in Math
JC Cut Off Points
Read more about JC Cut Off Points here: JC Cut Off Points
Taylor’s theorem with the Lagrange form of the remainder
There are countless situations in mathematics where it helps to expand a function as a power series. Therefore, Taylor’s theorem, which gives us circumstances under which this can be done, is an important result of the course. It is also the one result that I was dreading lecturing, at least with the Lagrange form of the remainder, because in the past I have always found that the proof is one that I have not been able to understand properly. I don’t mean by that that I couldn’t follow the arguments I read. What I mean is that I couldn’t reproduce the proof without committing a couple of things to memory, which I would then forget again once I had presented them. Briefly, an argument that appears in a lot of textbooks uses a result called the Cauchy mean value theorem, and applies it to a cleverly chosen function. Whereas I…
View original post 2,847 more words
PISA Is But One Education Indicator
guanyinmiao's musings (Archived: July 2009 to July 2019)
Following the announcement that Finnish students had under-performed in the Programme for International Student Assessment (PISA) – with scores dropping by 2.8, 1.7, and 3 per cent in mathematics, reading, and science respectively – the press release from the Ministry of Education and Culture read “PISA 2012: Proficiency of Finnish youth declining”. Minister Krista Kiuru has explained that a broad-based forum will be set up, for the “general downturn in learning outcomes shows that we must take strong action to develop Finnish education”.
In other words: not good enough, can do better.
On the other hand, Singapore’s Ministry of Education (MOE) proudly proclaimed that “International OECD Study Shows That Singapore Students Are Ready to Thrive in the 21st Century”. Indeed, the participating students have done well vis-à-vis their seniors and international counterparts, but it is debatable whether they can truly “solve problems in a variety of…
View original post 535 more words
Which Secondary School to Choose?
After receiving PSLE results, the next question would be: Which Secondary School to Choose?
Choosing the right secondary school is a big decision that will impact the next 4 (or more) years of life. And, the school with the highest PSLE Cut Off Points, may or may not be the best fit. Most important is to choose a school with a conducive learning environment so that the student can excel and perform to his/her fullest potential.
Read more information about that on the following websites:
1) PSLE: Top 3 things to remember when choosing a secondary school
2) Guide to Selecting a Secondary School for your child
(http://www.kiasuparents.com/kiasu/content/guide-selecting-secondary-school-your-child)
English Chinese Translation
We are offering online translation services from English to Chinese(Simplified).
Rates are negotiable and payable by Paypal.
The translation will be done by a professional translator, and after that vetted by myself.
Do feel free to contact us for more details. 🙂
SAT: Prep Books
Getting In: Blog for High School Students
Most Important SAT Book
The Official SAT Study Guide a.k.a. Blue Book, 2nd edition
The Official SAT Study Guide: Second Edition™ features 10 official SAT® practice tests created by the test maker.
SAT Strategy Book
SAT Prep Black Book: The Most Effective SAT Strategies Ever Published
The Black Book works best when used with the authentic SAT questions in the “Blue Book,” which is the College Board’s Official SAT Study Guide. The Black Book shows you how to beat the SAT, while the Blue Book gives you real SAT questions to practice with. Please buy College Board Blue Book to understand the strategies with questions from Blue Book.
SAT Math
Introductory SAT Math Book:
The New Math SAT Game Plan: The Strategic Way to Score Higher
A new edition, The New Math SAT Game Plan features updated strategy guides, more Algebra-II topics and all of those subversive tactics that have…
View original post 210 more words
SAT: Blogs and Websites
Getting In: Blog for High School Students
SAT Blogs/Websites
Excellent blog for SAT Math Tips and Tricks.
The Critical Reader
Another Excellent blog for SAT Grammar and Reading Tips and Tricks.
SparkNotes Free SAT Online Book
Excellent Free SAT Online Book covering SAT Math, Critical Reading and Writing Section.
Silverturtle’s Guide to SAT and Admissions Success
Excellent strategy guide from a student covering SAT and College Admission. It also included an excellent SAT Grammar section study guide.
SAT Subject Test: Biology E/M – Study Guide and Website
Getting In: Blog for High School Students
Websites
College Board SAT Biology E/M Practice Tests and Information Website
How to Study for the SAT Biology E/M Subject Test
Study Guides
Cracking the SAT Biology E/M Subject Test, 2013-2014 Edition
This book practice tests are more closer to real test.
Barron’s SAT Subject Test Biology E/M, 4th Edition
Barron Book has more details than Cracking the SAT Biology E/M Subject Test but questions are harder than real test.
Sparknotes Free Online SAT Biology E/M Subject Test Guide
Good introductory SAT Biology study guide
Singapore Maths Group Tuition for O Level 2014
https://mathtuition88.com/group-tuition/ https://mathtuition88.com/
Maths Tuition @ Bishan starting in 2014.
Secondary 4 O Level E Maths and A Maths.
Patient and Dedicated Maths Tutor (NUS Maths Major 1st Class Honours, Dean’s List, RI Alumni)
Email: mathtuition88@gmail.com
Free Exam Papers: https://mathtuition88.com/free-exam-papers/
Free Exam Paper
Awesome Mathematics Textbook!
Why is a negative divided by a negative a positive?
So there’s a whole lot of posts, including one from this very blog, which give intuitive explanations of why a negative times a negative is a positive.
I haven’t seen nearly as much material for a negative divided by a negative. One can certainly appeal to the inverse — since $latex 1 \times -1 = -1$, $latex \frac{-1}{-1} = 1$. Google searching leads to answers like that, but I’ve found nothing like the multiplication picture above.
Can anyone explain directly, at an intuitive level, why a negative divided by a negative is a positive? Or is the only way to do it to refer to multiplication?
Math: U of I Book Club-What’s Math Got to Do with It?
University of Idaho is offering a book club on What’s Math Got to Do with It?: How Parents and Teachers Can Help Children Learn to Love Their Least Favorite Subject by Jo Boaler.
The book club is free and includes a copy of the book! There is an option to participate for 1 credit offered through the University of Idaho for $60. Check out the flyer below and contact irmc@uidaho.edu to register.

Math Competition
Getting In: Blog for High School Students
American Mathematics Contest 10
The AMC 10 is a 25 question, 75 minute multiple choice examination in secondary school mathematics containing problems which can be understood and solved with algebra and geometry concepts.
American Mathematics Contest 12
The AMC 12 is a 25 question, 75 minute multiple choice examination in secondary school mathematics containing problems which can be understood and solved with pre-calculus concepts.
United States of America Mathematical Olympiad
The United States of America Mathematical Olympiad (USAMO) and the United States of America Junior Mathematical Olympiad (USAJMO) are six question, two day, 9 hour essay/proof examinations. All problems can be solved with pre-calculus methods. Approximately 270 of the top scoring AMC 12 participants (based on a weighted average of AMC 12 and AIME score) are invited to take the USAMO. Approximately 230 of the top scoring AMC 10 participants (based on a weighted average of AMC 10 and AIME…
View original post 158 more words
Surgery for Function Operations
My college algebra course boasts one of the driest textbooks on the planet. It’s one of those versions that has exercises from 1 to 99 for each section…brutal. Can you relate?
The topics for college algebra are very standard and cover little more than what students should have encountered recently in their algebra 2 course. I therefore decided that this class would lend itself quite nicely testing out the theory that a high-level, rich question questioning can be facilitated from a traditional, drill-and-kill style textbook.
Previously, I recall that Operations on Functions was a particularly awful topic for both me and my students. The textbook presents this concept in exactly the way you might think:
f(x) = [expression involving x] and g(x) = [similar expression involving x]
Find f(x) + g(x), f(x) – g(x), f(g(x), f(x) *g(x), f(x)/g(x)…f(snoozefest)…you get the point. It’s boring, they’ve done it before, and there’s…
View original post 346 more words
How to avoid careless mathematical errors?
I found this discussion on reddit “How to avoid careless mathematical errors?“:
Hi //math.
I am a high school student who happens to be VERY good at math, but who consistently fails to get As on tests due to careless errors. Most of the time, they come from forgetting a 0 after a decimal place, multiplying instead of dividing, putting a decimal point in the wrong place, or just factoring wrong. I actually had to drop a Precalc Honors class because I got Ds on tests from the sheer number of stupid mistakes I made, despite understanding the material very well.
I assume that this occurs because I work quickly, but if I work slowly, I run out of time on the test. Additionally, my handwriting is horrible, but there’s really nothing I can do about that. And even when I check my answers after finishing, I still…
View original post 639 more words
這是一個測試
1+2+3+4+…= -1/12!?
數學世界並不如一般人想象中的理性、不可抗逆。相反,很多表面上合理的論証,卻會引申出非常荒謬的結論。
其中一個我十分喜愛的算式如下:
最先論証這個看似荒謬的算式的人是印度著名數學家斯里尼瓦瑟.拉馬努金 (Srinivasa Ramanujan)。他提出的論証中牽涉到冪級數 (Power Series) 的運用。因此,我將會用一個比較易懂的方法,嘗試去証明這條算式是正確的。
首先設以上三項算式為S1、S2及S。
S1的答案比較易懂,從算式中可見,S1必定為 或 1 這兩個可能答案:
我們取 及 1 的平均數 1/2 為S1的答案 (假如取其平均數這做法令你感到很不安的話,事實上我有另一個論証方法可以証明 1/2 是最合理並最接近的答案,容後分解)。
然後將S2乘 2 ,算式如下:
兩列算式的數字各自相加後得出的結果如下:
很眼熟吧?沒錯,從以上計算中可以歸納出 2 x S2 = S1
而由於S1 = 1/2,代入以上算式可以得出 S2 = 1/4
之後,我們進行 S – S2 這一操作,運算過程如下:
奇妙的事情就在這裡開始發生了。剛才我們証明了S2 = 1/4,因此
S – 1/4 = 4*S
3*S = -1/4
S = -1/12
亦即証明:
難以致信吧?假如你無法接受這個違反常識,卻又看似合理的論証結果,我可以很榮幸地告訴你,
你的質疑是非常合理。
因為上述所有推算過程中都犯下了一個數學世界的禁忌,就是嘗試對無限 (Infinity) 進行操作。
真相是,無限本身是一個概念,而不是一個數字。因此,假如一意孤行地對無限進行加減乘除等操作時,便會出現如上述般荒誕的結果,就像整個數學系統當機了一樣。
不過,並非所有無限都是不可操作的。例如收斂級數 (Convergent Series) 便是一個有求和答案的無窮數列。
(credit: Numberphile)
View original post 2 more words
Liberal Arts is Not Dead
 Kennesaw- Who says that Liberal Arts is dead? One day in 1637, a lawyer and amateur mathematician named Pierre de Fermat scribbled a curious note in his journal: “The equation xn+ yn = zn, where x, y, and z are positive integers, has no solution if n is greater than 2… I have discovered a most remarkable proof, but this margin is too narrow to contain it.”
Kennesaw- Who says that Liberal Arts is dead? One day in 1637, a lawyer and amateur mathematician named Pierre de Fermat scribbled a curious note in his journal: “The equation xn+ yn = zn, where x, y, and z are positive integers, has no solution if n is greater than 2… I have discovered a most remarkable proof, but this margin is too narrow to contain it.”
In his spare time, Fermat studied languages, classical literature and natural science. He also discovered the fundamental principle of analytic geometry. His methods for finding tangents to curves and their maximum and minimum points led him to be regarded as the inventor of the differential calculus. Through his correspondence with Blaise Pascal he was a co-founder of the theory of probability.
It took mankind over 350 years to prove Fermat’s last theorem.
Spend time today encouraging…
View original post 45 more words
Place Value, or Thank You Hindus and Arabs, or The Beauty of the Base-Ten Numeration System
I have been doing a lot of thinking about place value lately. Yes, I need a life outside my standard state-issue gray cubicle. Nonetheless, I have become caught up in the beauty of the Hindu-Arabic number system. We also know it as the Base-Ten numeration system. It is beautiful and elegant. Let me elucidate (I love that word!)
One of the best t-shirts I have ever seen had this quote on the front, “There are only 10 kinds of people in the world; those who understand binary and those who don’t.” Some of you might be laughing right now while others are scratching their heads wondering what is wrong with me. Okay, here’s the joke. Binary is a base-2 numeration system. It has two digits – 0 and 1. Place value in binary is determined by powers of 2. So, in the units place you can have 0 and…
View original post 2,116 more words
A couple of notes on convergent series
Note: I originally published this entry on a Google Sites page in September 2013, but I have moved it hear as I hope to make better use of the $latex \LaTeX$ support offered by wordpress.com
I completed the first year of my maths degree in June 2013. I studied Analysis in all three terms (sequences and series in the first term, continuity and differentiability in the second, and Riemann integration in the third) and feel I have learnt a lot. Occasionally, amongst all this theory, I must admit to sometimes having lost touch with the original questions that provoked its development.
Consider the following naïve approach to infinite series. What is the answer if I add 1 and -1 alternately forever? That is
$latex \displaystyle{1+(-1)+1+(-1)+ … = ???}$
If I bracket the terms in pairs starting with the first and second terms, the answer appears to be 0:
$latex…
View original post 757 more words
Pi Number Approximation With Monte Carlo Method
Pi(Π) number is irrational and equal to 3.14159265… .
Let us draw a circle with radius ‘r’
$latex \int_0^{2\pi} r \mathrm{d}\theta = {2\pi} r &s=2$
So, circumference of the circle is equal to $latex {2\pi} r $
If the value of circumference is divided by value of diameter, the result is $latex \pi $
Area of quarter circle = $latex \frac{\pi r^2}{4}&s=2$
Area of the square = $latex {r^2}&s=2$
Probability of putting a dot on quarter circle is shown below.
$latex \frac{\frac{\pi r^2}{4}}{r^2} = \frac{\pi}{4}&s=3$
The area of circle is divided by total area.
In order to achieve $latex \pi $ value the result is multiplied by 4.
We can use Monte Carlo method for approximation $latex \pi $ value. For example, 10000 dots will be put on picture above. Each dot…
View original post 47 more words
Read All About It – Using Story and Picture Books in Maths Lessons

This blog was my very first venture into blogging on the fabulous Primary English blog. I’m very grateful to them for publishing it last May which led to me thinking seriously about starting my own blog. Their site is well worth a visit and they also have some amazing pinterest boards on all sorts of themes.
Here is what I blogged back in May:
As a maths leader, I quite often have the privilege of doing planning trawls and looking at weekly and medium term planning from other teachers. I’m often very impressed by the thought and detail that goes into these. But there’s one section that seems very rarely to be given much thought. If your weekly or medium term planning format is anything like mine, there’s a small section headed ‘cross-curricular links’, and I hardly ever see it filled in, except perhaps with the suggestions…
View original post 654 more words
Mathematical Methods for Quantitative Finance
Link: https://www.coursera.org/course/mathematicalmethods
Coverage: the official description is thorough. The caveat is that all topics are discussed without going too much into subtleties.
Potential audience: people with moderate knowledge of multivariable calculus, linear algebra and a bit of R programming experience who want to see how this knowledge may be applied to finance.
Format:
- a lecture; slides of lectures can be downloaded
- in-video questions
- a problem set; answers are provided for most problems
- a quiz; usually, it’s easier than the problem set
Note that only quizzes are graded.
Workload: 2-3 hours assuming you know calculus & linear algebra. If you don’t, then it’s hard to say.
Misc:
- there is no Statement of Accomplishment
- there is no course staff to help you, i.e. you should rely only on the assistance from your fellow courserians
- there are some misprints in materials. Hope Dr.Konis will have them fixed before the next session.
To sum…
View original post 33 more words
Monkey typing ABRACADABRA
Since I decided to call this blog martingalemeasure it seems only fitting that the first post should be about probability; martingales in particular. In my favorite introductory book on measure theoretical probability, “Probablity with Martingales” by David Williams, we find an exercise in Chapter 10, which I paraphrase here:
Suppose a monkey is typing randomly at a typewriter whose only keys are the capital letters $latex A$ through $latex Z$ of the english alphabet. What is the expected (average) time it will take for the monkey to type the word $latex ABRACADABRA$?
This is not an easy problem. In fact it’s not entirely obvious that the average time is even finte! Williams expects the reader to solve it using the beautiful theory of martingales and in particular Doob’s optional-stopping theorem. We will calculate the result below, but stop short of a proof. (There are many proofs of this result…
View original post 1,252 more words
A better way to calculate the day of the week
Geoff Canyon's Appeal to Authority
Look Like a Genius
Calculating the day of the week for historical date is impressive, but it isn’t as hard as it seems. Several methods have been shown to work and be performable by average humans. This is an improvement to one of the simplest methods.
The Doomsday Rule
Paraphrased from wikipedia:
The Doomsday rule or Doomsday algorithm is a relatively simple way to calculate the day of the week of a given date. It was devised by John Conway, drawing inspiration from Lewis Carroll’s work on a perpetual calendar algorithm. The algorithm takes advantage of the fact that several easy-to-remember dates fall on the same day each year; for example, 4/4, 6/6, 8/8, 10/10, 12/12, and the last day of February are all the same day of the week.
Conway’s original algorithm required dividing by 12 and 4, and remembering several intermediate values. It’s achievable, but not…
View original post 622 more words
Finding the distance between two points when the rate of a function is known
It’s About the Process: Not the Answer
When I first started teaching, I was always looking for the correct answer on a math problem. I would mark it wrong or right, there was no gray area. I began to change my thinking a bit when I noticed my students weren’t really growing. I knew that I needed to do something differently, so I began to start looking at the process of their thinking so that I could give direct feedback to help them get better.
If you think about it, we do the same thing in reading. We don’t expect students to become perfect readers overnight, so we give them reading strategies to become better. We look at their fluency, comprehension, how they monitor and self correct…we intervene and give feedback to help them.
With problem solving it can be the same way. We can take a look at the work a student writes down and see…
View original post 209 more words
What we didn’t know about Pythagoras
A really interesting and creative video about Pythagoras and the Pythagorean Theorem. Showing us how maybe Pythagoras wasn’t as awesome as we thought he was.
An extremely well done and well thought out video, about math, history and beans.
Math goal 3
Use a checklist to moniter my students’ understanding of fractions.
We have a unit test coming up at the end of the week on fractions. All throuout this week we will be working in small groups with students and I want to ensure that I am targeting my instruction to the concepts students need to review.
Reflection: I had some difficulties with this goal, but I definitely want to try this again another time. First, it was difficult for me to gauge the entire class in the short time I was using my checklist. For various reasons, I was only able to use it through portions of two lessons. The main problem I could see was that, since this was the end of the unit, I was not able to gather data on everything we had covered. Although, that is what I was trying to do with my ten item…
View original post 437 more words