Very nice introduction to Cohomology (8 min)

This is a very nice and concise 8 minute introduction to cohomology. Very clear and tells you the gist of cohomology.

Recommended Books for Spectral Sequences

Best Spectral Sequence Book

So far the most comprehensive book looks like McCleary’s book: A User’s Guide to Spectral Sequences. It is also suitable for those interested in the algebraic viewpoint. W.S. Massey wrote a very positive review to this book.

A User’s Guide to Spectral Sequences (Cambridge Studies in Advanced Mathematics)

Another book is Rotman’s An Introduction to Homological Algebra (Universitext). This book is from a homological algebra viewpoint. Rotman has a nice easy-going style, that made his books very popular to read.

The classic book may be MacLane’s Homology (Classics in Mathematics). This may be harder to read (though to be honest all books on spectral sequences are hard).

***Update: I found another book that gives a very nice presentation of certain spectral sequences, for instance the Bockstein spectral sequence. The book is Algebraic Methods in Unstable Homotopy Theory (New Mathematical Monographs) by Joseph Neisendorfer.

Topology application to Physics

Source: https://www.scientificamerican.com/article/the-strange-topology-that-is-reshaping-physics/?W

The Strange Topology That Is Reshaping Physics

Topological effects might be hiding inside perfectly ordinary materials, waiting to reveal bizarre new particles or bolster quantum computing

Charles Kane never thought he would be cavorting with topologists. “I don’t think like a mathematician,” admits Kane, a theoretical physicist who has tended to focus on tangible problems about solid materials. He is not alone. Physicists have typically paid little attention to topology—the mathematical study of shapes and their arrangement in space. But now Kane and other physicists are flocking to the field.

In the past decade, they have found that topology provides unique insight into the physics of materials, such as how some insulators can sneakily conduct electricity along a single-atom layer on their surfaces.

Some of these topological effects were uncovered in the 1980s, but only in the past few years have researchers begun to realize that they could be much more prevalent and bizarre than anyone expected. Topological materials have been “sitting in plain sight, and people didn’t think to look for them”, says Kane, who is at the University of Pennsylvania in Philadelphia.

Now, topological physics is truly exploding: it seems increasingly rare to see a paper on solid-state physics that doesn’t have the word topology in the title. And experimentalists are about to get even busier. A study on page 298 of this week’s Nature unveils an atlas of materials that might host topological effects, giving physicists many more places to go looking for bizarre states of matter such as Weyl fermions or quantum-spin liquids.

Read more at: https://www.scientificamerican.com/article/the-strange-topology-that-is-reshaping-physics/?WT.mc_id=SA_WR_20170726

Summary: Shapes, radius functions and persistent homology

This is a summary of a talk by Professor Herbert Edelsbrunner, IST Austria. The PDF slides can be found here: persistent homology slides.

Biogeometry (2:51 in video)

We can think of proteins as a geometric object by replacing every atom by a sphere (possibly different radii). Protein is viewed as union of balls in $\mathbb{R}^3$ .

Decompose into Voronoi domains $V(x)$ , and take the nerve (Delaunay complex).

Inclusion-Exclusion Theorem: $\displaystyle Vol(\bigcup B)=\sum_{Q\in D_r(x)}(-1)^{\dim Q}Vol(\bigcap Q).$
Volume of protein $(\bigcup B)$ is alternating sum over all simplices $Q$ in Delaunay complex.

Nerve Theorem: Union of sets have same homotopy type as nerve (stronger than having isomorphic homology groups).

Wrap (14:04 in video)

Collapses: 01 collapse means 0 dimensional and 1 dimensional simplices disappear (something like deformation retract).

Interval: Simplices that are removed in a collapse (always a skeleton of a cube in appropriate dimension)

Generalised Discrete Morse Function (Forman 1998): Generalised discrete vector field $=$ partition into intervals (for acyclic case only)

Critical simplex: The only simplex in an interval (when a critical simplex is added, the homotopy type changes)

Lower set of critical simplex: all the nodes that lead up to the critical simplex.

Wrap complex is the union of lower sets.

Persistence (38:00 in video)

Betti numbers in $\mathbb{R}^3$ : $\beta_0: \#$ components, $\beta_1:\#$ loops, $\beta_2: \#$ voids.

Incremental Algorithm to compute Betti numbers (40:50 in video). [Deffimado, E., 1995]. Every time a simplex is added, either a Betti number goes up (birth) or goes down (death).

$\alpha$ is born when it is not in image of previous homology group.

Stability of persistence: small change in position of points leads to similar persistence diagram.

Bottleneck distance between two diagrams is length of longest edge in minimizing matching. Theorem: $\displaystyle W_\infty(Dgm(f),Dgm(g))\leq\|f-g\|_\infty.$ [Cohen-Steiner, E., Hares 2007]. One of the most important theorems in persistent homology.

Expectation (51:30 in video)

Poisson point process: Like uniform distribution but over entire space. Number of points in region is proportional to size of region. Proportionality constant is density $\rho>0$ .

Paper: Expectations in $\mathbb{R}^n$ . [E., Nikitenko, Reitones, 2016]

Reduces to question (Three points in circle): Given three points in a circle, what is the probability that the triangle (with the 3 points as vertices) contains the center of the circle? Ans: 1/4 [Wendel 1963].

Brain has 11 dimensions

One of the possible applications of algebraic topology is in studying the brain, which is known to be very complicated.

Site: https://www.wired.com/story/the-mind-boggling-math-that-maybe-mapped-the-brain-in-11-dimensions/

If you can call understanding the dynamics of a virtual rat brain a real-world problem. In a multimillion-dollar supercomputer in a building on the same campus where Hess has spent 25 years stretching and shrinking geometric objects in her mind, lives one of the most detailed digital reconstructions of brain tissue ever built. Representing 55 distinct types of neurons and 36 million synapses all firing in a space the size of pinhead, the simulation is the brainchild of Henry Markram.

Markram and Hess met through a mutual researcher friend 12 years ago, right around the time Markram was launching Blue Brain—the Swiss institute’s ambitious bid to build a complete, simulated brain, starting with the rat. Over the next decade, as Markram began feeding terabytes of data into an IBM supercomputer and reconstructing a collection of neurons in the sensory cortex, he and Hess continued to meet and discuss how they might use her specialized knowledge to understand what he was creating. “It became clearer and clearer algebraic topology could help you see things you just can’t see with flat mathematics,” says Markram. But Hess didn’t officially join the project until 2015, when it met (and some would say failed) its first big public test.

In October of that year, Markram led an international team of neuroscientists in unveiling the first Blue Brain results: a simulation of 31,000 connected rat neurons that responded with waves of coordinated electricity in response to an artificial stimulus. The long awaited, 36-page paper published in Cell was not greeted as the unequivocal success Markram expected. Instead, it further polarized a research community already divided by the audacity of his prophesizing and the insane amount of money behind the project.

Two years before, the European Union had awarded Markram $1.3 billion to spend the next decade building a computerized human brain. But not long after, hundreds of EU scientists revolted against that initiative, the Human Brain Project. In the summer of 2015, they penned an open letter questioning the scientific value of the project and threatening to boycott unless it was reformed. Two independent reviews agreed with the critics, and the Human Brain Project downgraded Markram’s involvement. It was into this turbulent atmosphere that Blue Brain announced its modest progress on its bit of simulated rat cortex.

Guide to Starting Javaplex (With Matlab)

Step 1)

Visit https://appliedtopology.github.io/javaplex/ and download the Persistent Homology and Topological Data Analysis Library

Download the tutorial at http://www.math.colostate.edu/~adams/research/javaplex_tutorial.pdf and jump to section 1.3. Installation for Matlab.

In Matlab, change Matlab’s “Current Folder” to the directory matlab examples that you just extracted from the zip file.

(See https://www.mathworks.com/help/matlab/ref/cd.html to change current folder)

Type this in Matlab: cd /…/matlab_examples

Where … depends on where you put the folder

4) In the tutorial (from the link given in step 2), proceed to follow the instructions starting from “In Matlab, change Matlab’s “Current Folder” to the directory matlab examples that you just extracted from the zip file. In the Matlab command window, run the load javaplex.m file.”.

5) Test: Run example 3.2 (House example) by typing in the code (following the tutorial)

How the Staircase Diagram changes when we pass to derived couple (Spectral Sequence)

Set $A_{n,p}^1=H_n(X_p)$ and $E_{n,p}^1=H_n(X_p,X_{p-1})$ . The diagram then has the following form:

When we pass to the derived couple, each group $A_{n,p}^1$ is replaced by a subgroup $A_{n,p}^2=\text{Im}\,(i_1: A_{n,p-1}^1\to A_{n,p}^1)$ . The differentials $d_1=j_1k_1$ go two units to the right, and we replace the term $E_{n,p}^1$ by the term $E_{n,p}^2=\text{Ker}\, d_1/\text{Im}\,d_1$ , where the $d_1$ ‘s refer to the $d_1$ ‘s leaving and entering $E_{n,p}^1$ respectively.

The maps $j_2$ now go diagonally upward because of the formula $j_2(i_1a)=[j_1a]$ . The maps $i_2$ and $k_2$ still go vertically and horizontally, $i_2$ being a restriction of $i_1$ and $k_2$ being induced by $k_1$ .

Relative Homology Groups

Given a space $X$ and a subspace $A\subset X$ , define $C_n(X,A):=C_n(X)/C_n(A)$ . Since the boundary map $\partial: C_n(X)\to C_{n-1}(X)$ takes $C_n(A)$ to $C_{n-1}(A)$ , it induces a quotient boundary map $\partial: C_n(X,A)\to C_{n-1}(X,A)$ .

We have a chain complex $\displaystyle \dots\to C_{n+1}(X,A)\xrightarrow{\partial_{n+1}}C_n(X,A)\xrightarrow{\partial_n}C_{n-1}(X,A)\to\dots$ where $\partial^2=0$ holds. The relative homology groups $H_n(X,A)$ are the homology groups $\text{Ker}\,\partial_n/\text{Im}\,\partial_{n+1}$ of this chain complex.

Relative cycles
Elements of $H_n(X,A)$ are represented by relative cycles: $n$ – chains $\alpha\in C_n(X)$ such that $\partial\alpha\in C_{n-1}(A)$ .

Relative boundary
A relative cycle $\alpha$ is trivial in $H_n(X,A)$ iff it is a relative boundary: $\alpha=\partial\beta+\gamma$ for some $\beta\in C_{n+1}(X)$ and $\gamma\in C_n(A)$ .

Long Exact Sequence (Relative Homology)
There is a long exact sequence of homology groups:
$\begin{aligned} \dots\to H_n(A)\xrightarrow{i_*}H_n(X)\xrightarrow{j_*}H_n(X,A)\xrightarrow{\partial}H_{n-1}(A)&\xrightarrow{i_*}H_{n-1}(X)\to\dots\\ &\dots\to H_0(X,A)\to 0. \end{aligned}$

The boundary map $\partial:H_n(X,A)\to H_{n-1}(A)$ is as follows: If a class $[\alpha]\in H_n(X,A)$ is represented by a relative cycle $\alpha$ , then $\partial[\alpha]$ is the class of the cycle $\partial\alpha$ in $H_{n-1}(A)$ .

Exact sequence (Quotient space)

Exact sequence (Quotient space)
If $X$ is a space and $A$ is a nonempty closed subspace that is a deformation retract of some neighborhood in $X$ , then there is an exact sequence
$\begin{aligned} \dots\to\widetilde{H}_n(A)\xrightarrow{i_*}\widetilde{H}_n(X)\xrightarrow{j_*}\widetilde{H}_n(X/A)\xrightarrow{\partial}\widetilde{H}_{n-1}(A)&\xrightarrow{i_*}\widetilde{H}_{n-1}(X)\to\dots\\ &\dots\to\widetilde{H}_0(X/A)\to 0 \end{aligned}$
where $i$ is the inclusion $A\to X$ and $j$ is the quotient map $X\to X/A$ .

Reduced homology of spheres (Proof)
$\widetilde{H}_n(S^n)\cong\mathbb{Z}$ and $\widetilde{H}_i(S^n)=0$ for $i\neq n$ .

For $n>0$ take $(X,A)=(D^n,S^{n-1})$ so that $X/A=S^n$ . The terms $\widetilde{H}_i(D^n)$ in the long exact sequence are zero since $D^n$ is contractible.

Exactness of the sequence then implies that the maps $\widetilde{H}_i(S^n)\xrightarrow{\partial}\widetilde{H}_{i-1}(S^{n-1})$ are isomorphisms for $i>0$ and that $\widetilde{H}_0(S^n)=0$ . Starting with $\widetilde{H}_0(S^0)=\mathbb{Z}$ , $\widetilde{H}_i(S^0)=0$ for $i\neq 0$ , the result follows by induction on $n$ .

Reduced Homology

Define the reduced homology groups $\widetilde{H}_n(X)$ to be the homology groups of the augmented chain complex $\displaystyle \dots\to C_2(X)\xrightarrow{\partial_2}C_1(X)\xrightarrow{\partial_1}C_0(X)\xrightarrow{\epsilon}\mathbb{Z}\to 0$ where $\epsilon(\sum_i n_i\sigma_i)=\sum_in_i$ . We require $X$ to be nonempty, to avoid having a nontrivial homology group in dimension -1.

Relation between $H_n$ and $\widetilde{H}_n$
Since $\epsilon\partial_1=0$ , $\epsilon$ vanishes on $\text{Im}\,\partial_1$ and hence induces a map $\tilde{\epsilon}:H_0(X)\to\mathbb{Z}$ with $\ker\tilde{\epsilon}=\ker\epsilon/\text{Im}\,\partial_1=\widetilde{H}_0(X)$ . So $H_0(X)\cong\widetilde{H}_0(X)\oplus\mathbb{Z}$ . Clearly, $H_n(X)\cong\widetilde{H}_n(X)$ for $n>0$ .

Klein Bottle as Gluing of Two Mobius Bands

This is a nice picture on how the Klein bottle can be formed by gluing two Mobius bands together. Very neat and self-explanatory!

Source: https://math.stackexchange.com/questions/907176/klein-bottle-as-two-m%C3%B6bius-strips

Mayer-Vietoris Sequence applied to Spheres

Mayer-Vietoris Sequence
For a pair of subspaces $A,B\subset X$ such that $X=\text{int}(A)\cup\text{int}(B)$ , the exact MV sequence has the form
$\begin{aligned} \dots&\to H_n(A\cap B)\xrightarrow{\Phi}H_n(A)\oplus H_n(B)\xrightarrow{\Psi}H_n(X)\xrightarrow{\partial}H_{n-1}(A\cap B)\\ &\to\dots\to H_0(X)\to 0. \end{aligned}$

Example: $S^n$
Let $X=S^n$ with $A$ and $B$ the northern and southern hemispheres, so that $A\cap B=S^{n-1}$ . Then in the reduced Mayer-Vietoris sequence the terms $\tilde{H}_i(A)\oplus\tilde{H}_i(B)$ are zero. So from the reduced Mayer-Vietoris sequence $\displaystyle \dots\to\tilde{H}_i(A)\oplus\tilde{H}_i(B)\to\tilde{H}_i(X)\to\tilde{H}_{i-1}(A\cap B)\to\tilde{H}_{i-1}(A)\oplus\tilde{H}_{i-1}(B)\to\dots$ we get the exact sequence $\displaystyle 0\to\tilde{H}_i(S^n)\to\tilde{H}_{i-1}(S^{n-1})\to 0.$
We obtain isomorphisms $\tilde{H}_i(S^n)\cong\tilde{H}_{i-1}(S^{n-1})$ .

Spectral Sequence

Spectral Sequence is one of the advanced tools in Algebraic Topology. The following definition is from Hatcher’s 5th chapter on Spectral Sequences. The staircase diagram looks particularly impressive and intimidating at the same time.

Unfortunately, my LaTeX to WordPress Converter app can’t handle commutative diagrams well, so I will upload a printscreen instead.

Echelon Form Lemma (Column Echelon vs Smith Normal Form)

The pivots in column-echelon form are the same as the diagonal elements in (Smith) normal form. Moreover, the degree of the basis elements on pivot rows is the same in both forms.

Proof:
Due to the initial sort, the degree of row basis elements $\hat{e}_i$ is monotonically decreasing from the top row down. For each fixed column $j$ , $\deg e_j$ is a constant. We have, $\deg M_k(i,j)=\deg e_j-\deg \hat{e}_i$ . Hence, the degree of the elements in each column is monotonically increasing with row. That is, for fixed $j$ , $\deg M_k(i,j)$ is monotonically increasing as $i$ increases.

We may then eliminate non-zero elements below pivots using row operations that do not change the pivot elements or the degrees of the row basis elements. Finally, we place the matrix in (Smith) normal form with row and column swaps.

Persistent Homology Algorithm

Algorithm for Fields
In this section we describe an algorithm for computing persistent homology over a field.

We use the small filtration as an example and compute over $\mathbb{Z}_2$ , although the algorithm works for any field.
A filtered simplicial complex with new simplices added at each stage. The integers on the bottom row corresponds to the degrees of the simplices of the filtration as homogenous elements of the persistence module.

The persistence module corresponds to a $\mathbb{Z}_2[t]$ -module by the correspondence in previous Theorem. In this section we use $\{e_j\}$ and $\{\hat{e}_i\}$ to denote homogeneous bases for $C_k$ and $C_{k-1}$ respectively.

We have $\partial_1(ab)=-t\cdot a+t\cdot b=t\cdot a+t\cdot b$ since we are computing over $\mathbb{Z}_2$ . Then the representation matrix for $\partial_1$ is
$\displaystyle M_1=\begin{bmatrix}[c|ccccc] &ab &bc &cd &ad &ac\\ \hline d & 0 & 0 & t & t & 0\\ c & 0 & 1 & t & 0 & t^2\\ b & t & t & 0 & 0 & 0\\ a &t &0 &0 &t^2 &t^3 \end{bmatrix}.$

In general, any representation $M_k$ of $\partial_k$ has the following basic property: $\displaystyle \deg\hat{e}_i+\deg M_k(i,j)=\deg e_j$ provided $M_k(i,j)\neq 0$ .

We need to represent $\partial_k: C_k\to C_{k-1}$ relative to the standard basis for $C_k$ and a homogenous basis for $Z_{k-1}=\ker\partial_{k-1}$ . We then reduce the matrix according to the reduction algorithm described previously.

We compute the representations inductively in dimension. Since $\partial_0\equiv 0$ , $Z_0=C_0$ hence the standard basis may be used to represent $\partial_1$ . Now, suppose we have a matrix representation $M_k$ of $\partial_k$ relative to the standard basis $\{e_j\}$ for $C_k$ and a homogeneous basis $\{\hat{e}_i\}$ for $Z_{k-1}$ .

For the inductive step, we need to compute a homogeneous basis for $Z_k$ and represent $\partial_{k+1}$ relative to $C_{k+1}$ and the homogeneous basis for $Z_k$ . We first sort the basis $\hat{e}_i$ in reverse degree order. Next, we make $M_k$ into the column-echelon form $\tilde{M}_k$ by Gaussian elimination on the columns, using elementary column operations. From linear algebra, we know that $rank M_k=rank B_{k-1}$ is the number of pivots in the echelon form. The basis elements corresponding to non-pivot columns form the desired basis for $Z_k$ .

Source: “Computing Persistent Homology” by Zomorodian & Carlsson

De Rham Cohomology

De Rham Cohomology is a very cool sounding term in advanced math. This blog post is a short introduction on how it is defined.

Also, do check out our presentation on the relation between De Rham Cohomology and physics: De Rham Cohomology.

Definition:
A differential form $\omega$ on a manifold $M$ is said to be closed if $d\omega=0$ , and exact if $\omega=d\tau$ for some $\tau$ of degree one less.

Corollary:
Since $d^2=0$ , every exact form is closed.

Definition:
Let $Z^k(M)$ be the vector space of all closed $k$ -forms on $M$ .

Let $B^k(M)$ be the vector space of all exact $k$ -forms on $M$ .

Since every exact form is closed, hence $B^k(M)\subseteq Z^k(M)$ .

The de Rham cohomology of $M$ in degree $k$ is defined as the quotient vector space $\displaystyle H^k(M):=Z^k(M)/B^k(M).$

The quotient vector space construction induces an equivalence relation on $Z^k(M)$ :

$w'\sim w$ in $Z^k(M)$ iff $w'-w\in B^k(M)$ iff $w'=w+d\tau$ for some exact form $d\tau$ .

The equivalence class of a closed form $\omega$ is called its cohomology class and denoted by $[\omega]$ .

Singular Homology

A singular $n$ -simplex in a space $X$ is a map $\sigma: \Delta^n\to X$ . Let $C_n(X)$ be the free abelian group with basis the set of singular $n$ -simplices in $X$ . Elements of $C_n(X)$ , called singular $n$ -chains, are finite formal sums $\sum_i n_i\sigma_i$ for $n_i\in\mathbb{Z}$ and $\sigma_i: \Delta^n\to X$ . A boundary map $\partial_n: C_n(X)\to C_{n-1}(X)$ is defined by $\displaystyle \partial_n(\sigma)=\sum_i(-1)^i\sigma|[v_0,\dots,\widehat{v_i},\dots,v_n].$

The singular homology group is defined as $H_n(X):=\text{Ker}\partial_n/\text{Im}\partial_{n+1}$ .

Mapping Cone Theorem

Mapping cone
Let $f:(X,x_0)\to (Y,y_0)$ be a map in $\mathscr{PT}$ . We construct the mapping cone $Y\cup_f CX=Y\vee CX/\sim$ , where $[1,x]\in CX$ is identified with $f(x)\in Y$ for all $x\in X$ .

Proposition:
For any map $g: (Y,y_0)\to (Z,z_0)$ we have $g\circ f\simeq z_0$ if and only if $g$ has an extension $h: (Y\cup_f CX,*)\to(Z,z_0)$ to $Y\cup_f CX$ .

Proof:
By an earlier proposition (2.32 in \cite{Switzer2002}), $g\circ f\simeq z_0$ iff $g\circ f$ has an extension $\psi: (CX,*)\to (Z,z_0)$ .

( $\implies$ ) If $g\circ f\simeq z_0$ , define $\tilde{h}: Y\vee CX\to Z$ by $\tilde{h}(y_0,[t,x])=\psi[t,x]$ , $\tilde{h}(y,[0,x])=g(y)$ . Note that $\tilde{h}(y_0,[0,x])=\psi[0,x]=g(y_0)=z_0$ . Since $\displaystyle \tilde{h}(y_0,[1,x])=\psi[1,x]=gf(x)=\tilde{h}(f(x),[0,x]),$ $\tilde{h}$ induces a map $h: Y\cup_f CX\to Z$ which satisfies $h[y,[0,x]]=\tilde{h}(y,[0,x])=g(y)$ . That is $h|_Y=g$ .

( $\impliedby$ ) If $g$ has an extension $h: (Y\cup_f CX,*)\to (Z,z_0)$ , then define $\psi: CX\to Z$ by $\psi([t,x])=h[y_0,[t,x]]$ . We have $\psi([0,x])=h[y_0,[0,x]]=z_0$ . Then $\displaystyle \psi([1,x])=h[y_0,[1,x]]=h[f(x),[0,x]]=gf(x).$ That is, $\psi|_X=g\circ f$ .

Tangent space (Derivation definition)

Let $M$ be a smooth manifold, and let $p\in M$ . A linear map $v: C^\infty(M)\to\mathbb{R}$ is called a derivation at $p$ if it satisfies $\displaystyle v(fg)=f(p)vg+g(p)vf\qquad\text{for all}\ f,g\in C^\infty(M).$
The tangent space to $M$ at $p$ , denoted by $T_pM$ , is defined as the set of all derivations of $C^\infty(M)$ at $p$ .

Homology Group of some Common Spaces

Homology of Circle
$\displaystyle H_n(S^1)=\begin{cases}\mathbb{Z}&\text{for}\ n=0,1\\ 0&\text{for}\ n\geq 2. \end{cases}$

Homology of Torus
$\displaystyle H_n(T)=\begin{cases}\mathbb{Z}\oplus\mathbb{Z}&\text{for}\ n=1\\ \mathbb{Z}&\text{for}\ n=0, 2\\ 0&\text{for}\ n\geq 3. \end{cases}$

Homology of Real Projective Plane
$\displaystyle H_n(\mathbb{R}P^2)=\begin{cases} \mathbb{Z}&\text{for}\ n=0\\ \mathbb{Z}_2&\text{for}\ n=1\\ 0&\text{for}\ n\geq 2. \end{cases}$

Homology of Klein Bottle
$\displaystyle H_n(K)=\begin{cases} \mathbb{Z}&\text{for}\ n=0\\ \mathbb{Z}_2\oplus\mathbb{Z}&\text{for}\ n=1\\ 0&\text{for}\ n\geq 2. \end{cases}$

Also see How to calculate Homology Groups (Klein Bottle).

Summary of Persistent Homology

We summarize the work so far and relate it to previous results. Our input is a filtered complex $K$ and we wish to find its $k$ th homology $H_k$ . In each dimension the homology of complex $K^i$ becomes a vector space over a field, described fully by its rank $\beta_k^i$ . (Over a field $F$ , $H_k$ is a $F$ -module which is a vector space.)

We need to choose compatible bases across the filtration (compatible bases for $H_k^i$ and $H_k^{i+p}$ ) in order to compute persistent homology for the entire filtration. Hence, we form the persistence module $\mathscr{M}$ corresponding to $K$ , which is a direct sum of these vector spaces ( $\alpha(\mathscr{M})=\bigoplus M^i$ ). By the structure theorem, a basis exists for this module that provides compatible bases for all the vector spaces.

Specifically, each $\mathcal{P}$ -interval $(i,j)$ describes a basis element for the homology vector spaces starting at time $i$ until time $j-1$ . This element is a $k$ -cycle $e$ that is completed at time $i$ , forming a new homology class. It also remains non-bounding until time $j$ , at which time it joins the boundary group $B_k^j$ .

A natural question is to ask when $e+B_k^l$ is a basis element for the persistent groups $H_k^{l,p}$ . Recall the equation $\displaystyle H_k^{i,p}=Z_k^i/(B_k^{i+p}\cap Z_k^i).$ Since $e\notin B_k^l$ for all $l<j$ , hence $e\notin B_k^{l+p}$ for $l+p<j$ . The three inequalities $\displaystyle l+p<j,\ l\geq i,\ p\geq 0$ define a triangular region in the index-persistence plane, as shown in Figure below.

The triangular region gives us the values for which the $k$ -cycle $e$ is a basis element for $H_k^{l,p}$ . This is known as the $k$ -triangle Lemma:

Let $\mathcal{T}$ be the set of triangles defined by $\mathcal{P}$ -intervals for the $k$ -dimensional persistence module. The rank $\beta_k^{l,p}$ of $H_k^{l,p}$ is the number of triangles in $\mathcal{T}$ containing the point $(l,p)$ .

Hence, computing persistent homology over a field is equivalent to finding the corresponding set of $\mathcal{P}$ -intervals.

Source: “Computing Persistent Homology” by Zomorodian and Carlsson

Structure Theorem for finitely generated (graded) modules over a PID

If $R$ is a PID, then every finitely generated module $M$ over $R$ is isomorphic to a direct sum of cyclic $R$ -modules. That is, there is a unique decreasing sequence of proper ideals $(d_1)\supseteq(d_2)\supseteq\dots\supseteq(d_m)$ such that $\displaystyle M\cong R^\beta\oplus\left(\bigoplus_{i=1}^m R/(d_i)\right)$ where $d_i\in R$ , and $\beta\in\mathbb{Z}$ .

Similarly, every graded module $M$ over a graded PID $R$ decomposes uniquely into the form $\displaystyle M\cong\left(\bigoplus_{i=1}^n\Sigma^{\alpha_i}R\right)\oplus\left(\bigoplus_{j=1}^m\Sigma^{\gamma_j}R/(d_j)\right)$ where $d_j\in R$ are homogenous elements such that $(d_1)\supseteq(d_2)\supseteq\dots\supseteq(d_m)$ , $\alpha_i, \gamma_j\in\mathbb{Z}$ , and $\Sigma^\alpha$ denotes an $\alpha$ -shift upward in grading.

Persistence Interval

Next, we want to parametrize the isomorphism classes of the $F[t]$ -modules by suitable objects.

A $\mathcal{P}$ -interval is an ordered pair $(i,j)$ with $0\leq i<j\in\mathbb{Z}^\infty=\mathbb{Z}\cup\{+\infty\}$ .

We may associate a graded $F[t]$ -module to a set $\mathcal{S}$ of $\mathcal{P}$ -intervals via a bijection $Q$ . We define $\displaystyle Q(i,j)=\Sigma^i F[t]/(t^{j-i})$ for a $\mathcal{P}$ -interval $(i,j)$ . When $j=+\infty$ , we have $Q(i,+\infty)=\Sigma^iF[t]$ .

For a set of $\mathcal{P}$ -intervals $\mathcal{S}=\{(i_1,j_1),(i_2,j_2),\dots,(i_n,j_n)\}$ , we define $\displaystyle Q(\mathcal{S})=\bigoplus_{k=1}^n Q(i_k, j_k).$

We may now restate the correspondence as follows.

The correspondence $\mathcal{S}\to Q(\mathcal{S})$ defines a bijection between the finite sets of $\mathcal{P}$ -intervals and the finitely generated graded modules over the graded ring $F[t]$ .

Hence, the isomorphism classes of persistence modules of finite type over $F$ are in bijective correspondence with the finite sets of $\mathcal{P}$ -intervals.

Homogenous / Graded Ideal

Let $A=\bigoplus_{i=0}^\infty A_i$ be a graded ring. An ideal $I\subset A$ is homogenous (also called graded) if for every element $x\in I$ , its homogenous components also belong to $I$ .

An ideal in a graded ring is homogenous if and only if it is a graded submodule. The intersections of a homogenous ideal $I$ with the $A_i$ are called the homogenous parts of $I$ . A homogenous ideal $I$ is the direct sum of its homogenous parts, that is, $\displaystyle I=\bigoplus_{i=0}^\infty (I\cap A_i).$

Persistence module and Graded Module

We show that the persistent homology of a filtered simplicial complex is the standard homology of a particular graded module over a polynomial ring.

First we review some definitions.

A graded ring is a ring $R=\bigoplus_i R_i$ (a direct sum of abelian groups $R_i$ ) such that $R_iR_j\subset R_{i+j}$ for all $i$ , $j$ .

A graded ring $R$ is called non-negatively graded if $R_n=0$ for all $n\leq 0$ . Elements of any factor $R_n$ of the decomposition are called homogenous elements of degree $n$ .

Polynomial ring with standard grading:
We may grade the polynomial ring $R[t]$ non-negatively with the standard grading $R_n=Rt^n$ for all $n\geq 0$ .

Graded module:
A graded module is a left module $M$ over a graded ring $R$ such that $M=\bigoplus_i M_i$ and $R_iM_j\subseteq M_{i+j}$ .

Let $R$ be a commutative ring with unity. Let $\mathscr{M}=\{M^i,\varphi^i\}_{i\geq 0}$ be a persistence module over $R$ .

We now equip $R[t]$ with the standard grading and define a graded module over $R[t]$ by $\displaystyle \alpha(\mathscr{M})=\bigoplus_{i=0}^\infty M^i$ where the $R$ -module structure is the sum of the structures on the individual components. That is, for all $r\in R$ , $\displaystyle r\cdot (m^0,m^1,m^2,\dots)=(rm^0,rm^1,rm^2,\dots).$

The action of $t$ is given by $\displaystyle t\cdot (m^0, m^1, m^2,\dots)=(0,\varphi^0(m^0),\varphi^1(m^1),\varphi^2(m^2),\dots).$
That is, $t$ shifts elements of the module up in the gradation.

Source: “Computing Persistent Homology” by Zomorodian and Carlsson.

Persistence module and Finite type

A persistence module $\mathcal{M}=\{M^i,\varphi^i\}_{i\geq 0}$ is a family of $R$ -modules $M^i$ , together with homomorphisms $\varphi^i: M^i\to M^{i+1}$ .

For example, the homology of a persistence complex is a persistence module, where $\varphi^i$ maps a homology class to the one that contains it.

A persistence complex $\{C_*^i, f^i\}$ (resp.\ persistence module $\{M^i, \varphi^i\}$ ) is of finite type if each component complex (resp.\ module) is a finitely generated $R$ -module, and if the maps $f^i$ (resp.\ $\varphi^i$ ) are isomorphisms for $i\geq m$ for some integer $m$ .

If $K$ is a finite filtered simplicial complex, then it generates a persistence complex $\mathscr{C}$ of finite type, whose homology is a persistence module $\mathcal{M}$ of finite type.

Homotopy for Maps vs Paths

Homotopy (of maps)

A homotopy is a family of maps $f_t: X\to Y$ , $t\in I$ , such that the associated map $F:X\times I\to Y$ given by $F(x,t)=f_t(x)$ is continuous. Two maps $f_0, f_1:X\to Y$ are called homotopic, denoted $f_0\simeq f_1$ , if there exists a homotopy $f_t$ connecting them.

Homotopy of paths

A homotopy of paths in a space $X$ is a family $f_t: I\to X$ , $0\leq t\leq 1$ , such that

(i) The endpoints $f_t(0)=x_0$ and $f_t(1)=x_1$ are independent of $t$ .
(ii) The associated map $F:I\times I\to X$ defined by $F(s,t)=f_t(s)$ is continuous.

When two paths $f_0$ and $f_1$ are connected in this way by a homotopy $f_t$ , they are said to be homotopic. The notation for this is $f_0\simeq f_1$ .

The above two definitions are related, since a path is a special kind of map $f: I\to X$ .

Universal Property of Quotient Groups (Hungerford)

If $f:G\to H$ is a homomorphism and $N$ is a normal subgroup of $G$ contained in the kernel of $f$ , then $f$ “factors through” the quotient $G/N$ uniquely.

This can be used to prove the following proposition:
A chain map $f_\bullet$ between chain complexes $(A_\bullet, \partial_{A, \bullet})$ and $(B_\bullet, \partial_{B,\bullet})$ induces homomorphisms between the homology groups of the two complexes.

Proof:
The relation $\partial f=f\partial$ implies that $f$ takes cycles to cycles since $\partial\alpha=0$ implies $\partial(f\alpha)=f(\partial\alpha)=0$ . Also $f$ takes boundaries to boundaries since $f(\partial\beta)=\partial(f\beta)$ . Hence $f_\bullet$ induces a homomorphism $(f_\bullet)_*: H_\bullet (A_\bullet)\to H_\bullet (B_\bullet)$ , by universal property of quotient groups.

For $\beta\in\text{Im} \partial_{A,n+1}$ , we have $\pi_{B,n}f_n(\beta)=\text{Im}\partial_{B,n+1}$ . Therefore $\text{Im}\partial_{A,n+1}\subseteq\ker(\pi_{B,n}\circ f_n)$ .

Some Homology Definitions

Chain Complex
A sequence of homomorphisms of abelian groups $\displaystyle \dots\to C_{n+1}\xrightarrow{\partial_{n+1}}C_n\xrightarrow{\partial_n}C_{n-1}\to\dots\to C_1\xrightarrow{\partial_1}C_0\xrightarrow{\partial_0}0$ with $\partial_n\partial_{n+1}=0$ for each $n$ .

$n$ th Homology Group
$H_n=\text{Ker}\,\partial_n/\text{Im}\,\partial_{n+1}$

$\Delta_n(X)$
$\Delta_n(X)$ is the free abelian group with basis the open $n$ -simplices $e_\alpha^n$ of $X$ .

$n$ -chains
Elements of $\Delta_n(X)$ , called $n$ -chains, can be written as finite formal sums $\sum_\alpha n_\alpha e_\alpha^n$ with coefficients $n_\alpha\in\mathbb{Z}$ .

Introduction to Persistent Homology (Cech and Vietoris-Rips complex)

Motivation
Data is commonly represented as an unordered sequence of points in the Euclidean space $\mathbb{R}^n$ . The global `shape’ of the data may provide important information about the underlying phenomena of the data.

For data points in $\mathbb{R}^2$ , determining the global structure is not difficult, but for data in higher dimensions, a planar projection can be hard to decipher.
From point cloud data to simplicial complexes
To convert a collection of points $\{x_\alpha\}$ in a metric space into a global object, one can use the points as the vertices of a graph whose edges are determined by proximity (vertices within some chosen distance $\epsilon$ ). Then, one completes the graph to a simplicial complex. Two of the most natural methods for doing so are as follows:

Given a set of points $\{x_\alpha\}$ in Euclidean space $\mathbb{R}^n$ , the Cech complex (also known as the nerve), $\mathcal{C}_\epsilon$ , is the abstract simplicial complex where a set of $k+1$ vertices spans a $k$ -simplex whenever the $k+1$ corresponding closed $\epsilon/2$ -ball neighborhoods have nonempty intersection.

Given a set of points $\{x_\alpha\}$ in Euclidean space $\mathbb{R}^n$ , the Vietoris-Rips complex, $\mathcal{R}_\epsilon$ , is the abstract simplicial complex where a set $S$ of $k+1$ vertices spans a $k$ -simplex whenever the distance between any pair of points in $S$ is at most $\epsilon$ .

Top left: A fixed set of points. Top right: Closed balls of radius $\epsilon/2$ centered at the points. Bottom left: Cech complex has the homotopy type of the $\epsilon/2$ cover ( $S^1\vee S^1\vee S^1$ ) Bottom right: Vietoris-Rips complex has a different homotopy type ( $S^1\vee S^2$ ). Image from R. Ghrist, 2008, Barcodes: The Persistent Topology of Data.

Natural Equivalence relating Suspension and Loop Space

Theorem:
If $(X,x_0)$ , $(Y,y_0)$ , $(Z,z_0)\in\mathscr{PT}$ , $X$ , $Z$ Hausdorff and $Z$ locally compact, then there is a natural equivalence $\displaystyle A: [Z\wedge X, *; Y,y_0]\to [X, x_0; (Y,y_0)^{(Z,z_0)}, f_0]$ defined by $A[f]=[\hat{f}]$ , where if $f:Z\wedge X\to Y$ is a map then $\hat{f}: X\to Y^Z$ is given by $(\hat{f}(x))(z)=f[z,x]$ .

We need the following two propositions in order to prove the theorem.
Proposition
\label{prop13}
The exponential function $E: Y^{Z\times X}\to (Y^Z)^X$ induces a continuous function $\displaystyle E: (Y,y_0)^{(Z\times X, Z\vee X)}\to ((Y,y_0)^{(Z,z_0)}, f_0)^{(X,x_0)}$ which is a homeomorphism if $Z$ and $X$ are Hausdorff and $Z$ is locally compact\footnote{every point of $Z$ has a compact neighborhood}.

Proposition
\label{prop8}
If $\alpha$ is an equivalence relation on a topological space $X$ and $F:X\times I\to Y$ is a homotopy such that each stage $F_t$ factors through $X/\alpha$ , i.e.\ $x\alpha x'\implies F_t(x)=F_t(x')$ , then $F$ induces a homotopy $F':(X/\alpha)\times I\to Y$ such that $F'\circ (p_\alpha\times 1)=F$ .

Proof of Theorem
i) $A$ is surjective: Let $f': (X,x_0)\to ((Y,y_0)^{(Z,z_0)},f_0)$ . From Proposition \ref{prop13} we have that $E: (Y,y_0)^{(Z\times X, Z\vee X)}\to ((Y,y_0)^{(Z,z_0)},f_0)^{(X,x_0)}$ is a homeomorphism. Hence the function $\bar{f}: (Z\times X, Z\vee X)\to (Y,y_0)$ defined by $\bar{f}(z,x)=(f'(x))(z)$ is continuous since $(Ef'(x))(z)=f'(z,x)$ and thus $\bar{f}=E^{-1}f'$ . By the universal property of the quotient, $\bar{f}$ defines a map $f:(Z\wedge X, *)\to (Y,y_0)$ such that $f[z,x]=\bar{f}(z,x)=(f'(x))(z)$ . Thus $\hat{f}=f'$ , so that $A[f]=[f']$ .

ii) $A$ is injective: Suppose $f,g: (Z\wedge X, *)\to (Y,y_0)$ are two maps such that $A[f]=A[g]$ , i.e.\ $\hat{f}\simeq\hat{g}$ . Let $H': X\times I\to (Y,y_0)^{(Z,z_0)}$ be the homotopy rel $x_0$ . By Proposition \ref{prop13} the function $\bar{H}: Z\times X\times I\to Y$ defined by $\bar{H}(z,x,t)=(H'(x,t))(z)$ is continuous. This is because $\bar{H}(z,x,t)=(E\bar{H}(x,t))(z)$ so that $E\bar{H}=H'$ , thus $\bar{H}=E^{-1}H'$ where $E$ is a homeomorphism. For each $t\in I$ we have $\bar{H}((Z\vee X)\times\{t\})=y_0$ . This is because if $(z,x)\in Z\vee X$ , then $z=z_0$ or $x=x_0$ . If $z=z_0$ , then $(H'(x,t))(z_0)=y_0$ . If $x=x_0$ , $(H'(x_0,t))(z)=y_0$ as $H'$ is the homotopy rel $x_0$ . Then by Proposition \ref{prop8} there is a homotopy $H:(Z\wedge X)\times I\to Y$ rel $*$ such that $H([z,x],t)=\bar{H}(z,x,t)=(H'(x,t))(z)$ . Thus $H_0([z,x])=(H_0'(x))(z)=(\hat{f}(x))(z)=f[z,x]$ and similarly $H_1([z,x])=(H_1'(x))(z)=(\hat{g}(x))(z)=g[z,x]$ . Thus $[f]=[g]$ via the homotopy $H$ .

Loop space
If $(Y,y_0)\in\mathscr{PT}$ , we define the loop space $(\Omega Y, \omega_0)\in\mathscr{PT}$ of $Y$ to be the function space $\displaystyle \Omega Y=(Y,y_0)^{(S^1,s_0)}$ with the constant loop $\omega_0$ ( $\omega_0(s)=y_0$ for all $s\in S^1$ ) as base point.

Suspension
If $(X,x_0)\in\mathscr{PT}$ , we define the suspension $(SX,*)\in\mathscr{PT}$ of $X$ to be the smash product $(S^1\wedge X, *)$ of $X$ with the 1-sphere.

Corollary (Natural Equivalence relating $SX$ and $\Omega Y$ )
If $(X,x_0)$ , $(Y,y_0)\in\mathscr{PT}$ and $X$ is Hausdorff, then there is a natural equivalence $\displaystyle A: [SX, *; Y,y_0]\to [X, x_0; \Omega Y, \omega_0].$

Fundamental Group of S^n is trivial if n>=2

$\pi_1(S^n)=0$ if $n\geq 2$
We need the following lemma:

If a space $X$ is the union of a collection of path-connected open sets $A_\alpha$ each containing the basepoint $x_0\in X$ and if each intersection $A_\alpha\cap A_\beta$ is path-connected, then every loop in $X$ at $x_0$ is homotopic to a product of loops each of which is contained in a single $A_\alpha$ .

Proof:
Take $A_1$ and $A_2$ to be the complements of two antipodal points in $S^n$ . Then $S^n=A_1\cup A_2$ is the union of two open sets $A_1$ and $A_2$ , each homeomorphic to $\mathbb{R}^n$ such that $A_1\cap A_2$ is homeomorphic to $S^{n-1}\times\mathbb{R}$ .

Choose a basepoint $x_0$ in $A_1\cap A_2$ . If $n\geq 2$ then $A_1\cap A_2$ is path-connected. By the lemma, every loop in $S^n$ based at $x_0$ is homotopic to a product of loops in $A_1$ or $A_2$ . Both $\pi_1(A_1)$ and $\pi_1(A_2)$ are zero since $A_1$ and $A_2$ are homeomorphic to $\mathbb{R}^n$ . Hence every loop in $S^n$ is nullhomotopic.

Functors, Homotopy Sets and Groups

Functors
Definition:
A functor $F$ from a category $\mathscr{C}$ to a category $\mathscr{D}$ is a function which
– For each object $X\in\mathscr{C}$ , we have an object $F(X)\in\mathscr{D}$ .
– For each $f\in\hom_\mathscr{C}(X,Y)$ , we have a morphism $\displaystyle F(f)\in\hom_\mathscr{D}(F(X),F(Y)).$

Furthermore, $F$ is required to satisfy the two axioms:
– For each object $X\in\mathscr{C}$ , we have $F(1_X)=1_{F(X)}$ . That is, $F$ maps the identity morphism on $X$ to the identity morphism on $F(X)$ .

– For $f\in\hom_{\mathscr{C}}(X,Y)$ , $g\in\hom_\mathscr{C}(Y,Z)$ we have $\displaystyle F(g\circ f)=F(g)\circ F(f)\in\hom_\mathscr{D}(F(X),F(Z)).$ That is, functors must preserve composition of morphisms.

Definition:
A cofunctor (also called contravariant functor) $F^*$ from a category $\mathscr{C}$ to a category $\mathscr{D}$ is a function which
– For each object $X\in\mathscr{C}$ , we have an object $F^*(X)\in\mathscr{D}$ .
– For each $f\in\hom_\mathscr{C}(X,Y)$ we have a morphism $\displaystyle F^*(f)\in\hom_\mathscr{D}(F^*(Y),F^*(X))$ satisfying the two axioms:
– For each object $X\in\mathscr{C}$ we have $F^*(1_X)=1_{F^*(X)}$ . That is, $F^*$ preserves identity morphisms.
– For each $f\in\hom_\mathscr{C}(X,Y)$ and $g\in\hom_\mathscr{C}(Y,Z)$ we have $\displaystyle F^*(g\circ f)=F^*(f)\circ F^*(g)\in\hom_\mathscr{D}(F^*(Z),F^*(X)).$ Note that cofunctors reverse the direction of composition.

Example

Given a fixed pointed space $(K,k_0)\in\mathscr{PT}$ , we define a functor $\displaystyle F_K:\mathscr{PT}\to\mathscr{PS}$ as follows: for each $(X,x_0)\in\mathscr{PT}$ we assign $F_K(X,x_0)=[K,k_0; X,x_0]\in\mathscr{PS}$ . Given $f: (X,x_0)\to (Y,y_0)$ in $\hom((X,x_0),(Y,y_0))$ we define $F_K(f)\in\hom([K,k_0; X,x_0],[K,k_0;Y,y_0])$ by $\displaystyle F_k(f)[g]=[f\circ g]\in[K,k_0; Y,y_0]$ for every $[g]\in [K,k_0; X,x_0]$ .

We can check the two axioms:
– $F_k(1_X)[g]=[1_X\circ g]=[g]$ for every $[g]\in[K,k_0; X, x_0]$ .
– For $f\in\hom((X,x_0),(Y,y_0))$ , $h\in\hom((Y,y_0),(Z,z_0))$ we have $\displaystyle F_K(h\circ f)[g]=[h\circ f\circ g]=F_K(h)\circ F_K(f)[g]\in[K,k_0; Z,z_0]$ for every $[g]\in[K,k_0; X,x_0]$ .

Similarly, we can define a cofunctor $F_K^*$ by taking $F_K^*(X,x_0)=[X,x_0; K,k_0]$ and for $f:(X,x_0)\to (Y,y_0)$ in $\hom((X,x_0),(Y,y_0))$ we define $\displaystyle F_K(f)[g]=[g\circ f]\in[X,x_0; K,k_0]$ for every $[g]\in[Y,y_0; K,k_0]$ .

Note that if $f\simeq f'$ rel $x_0$ , then $F_K(f)=F_K(f')$ and similarly $F_K^*(f)=F_K^*(f')$ . Therefore $F_K$ (resp.\ $F_K^*$ ) can also be regarded as defining a functor (resp.\ cofunctor) $\mathscr{PT}'\to\mathscr{PS}$ .

Homotopy Sets and Groups
Theorem:
If $(X,x_0)$ , $(Y,y_0)$ , $(Z,z_0)\in\mathscr{PT}$ , $X$ , $Z$ Hausdorff and $Z$ locally compact, then there is a natural equivalence $\displaystyle A: [Z\wedge X, *; Y,y_0]\to [X, x_0; (Y,y_0)^{(Z,z_0)}, f_0]$ defined by $A[f]=[\hat{f}]$ , where if $f:Z\wedge X\to Y$ is a map then $\hat{f}: X\to Y^Z$ is given by $(\hat{f}(x))(z)=f[z,x]$ .

We need the following two propositions in order to prove the theorem.

Proposition 1:
The exponential function $E: Y^{Z\times X}\to (Y^Z)^X$ induces a continuous function $\displaystyle E: (Y,y_0)^{(Z\times X, Z\vee X)}\to ((Y,y_0)^{(Z,z_0)}, f_0)^{(X,x_0)}$ which is a homeomorphism if $Z$ and $X$ are Hausdorff and $Z$ is locally compact\footnote{every point of $Z$ has a compact neighborhood}.

Proposition 2:
If $\alpha$ is an equivalence relation on a topological space $X$ and $F:X\times I\to Y$ is a homotopy such that each stage $F_t$ factors through $X/\alpha$ , i.e.\ $x\alpha x'\implies F_t(x)=F_t(x')$ , then $F$ induces a homotopy $F':(X/\alpha)\times I\to Y$ such that $F'\circ (p_\alpha\times 1)=F$ .

Algebraic Topology: Fundamental Group

Homotopy of paths
A homotopy of paths in a space $X$ is a family $f_t: I\to X$ , $0\leq t\leq 1$ , such that
(i) The endpoints $f_t(0)=x_0$ and $f_t(1)=x_1$ are independent of $t$ .
(ii) The associated map $F:I\times I\to X$ defined by $F(s,t)=f_t(s)$ is continuous.

When two paths $f_0$ and $f_1$ are connected in this way by a homotopy $f_t$ , they are said to be homotopic. The notation for this is $f_0\simeq f_1$ .

Example: Linear Homotopies
Any two paths $f_0$ and $f_1$ in $\mathbb{R}^n$ having the same endpoints $x_0$ and $x_1$ are homotopic via the homotopy $\displaystyle f_t(s)=(1-t)f_0(s)+tf_1(s).$

Simply-connected
A space is called simply-connected if it is path-connected and has trivial fundamental group.

A space $X$ is simply-connected iff there is a unique homotopy class of paths connecting any two parts in $X$ .
Path-connectedness is the existence of paths connecting every pair of points, so we need to be concerned only with the uniqueness of connecting paths.

( $\implies$ ) Suppose $\pi_1(X)=0$ . If $f$ and $g$ are two paths from $x_0$ to $x_1$ , then $f\simeq f\cdot \bar{g}\cdot g\simeq g$ since the loops $\bar{g}\cdot g$ and $f\cdot\bar{g}$ are each homotopic to constant loops, due to $\pi_1(X,x_0)=0$ .

( $\impliedby$ ) Conversely, if there is only one homotopy class of paths connecting a basepoint $x_0$ to itself, then all loops at $x_0$ are homotopic to the constant loop and $\pi_1(X,x_0)=0$ .

$\pi_1(X\times Y)$ is isomorphic to $\pi_1(X)\times \pi_1(Y)$ if $X$ and $Y$ are path-connected.
A basic property of the product topology is that a map $f:Z\to X\times Y$ is continuous iff the maps $g:Z\to X$ and $h:Z\to Y$ defined by $f(z)=(g(z),h(z))$ are both continuous.

Hence a loop $f$ in $X\times Y$ based at $(x_0,y_0)$ is equivalent to a pair of loops $g$ in $X$ and $h$ in $Y$ based at $x_0$ and $y_0$ respectively.

Similarly, a homotopy $f_t$ of a loop in $X\times Y$ is equivalent to a pair of homotopies $g_t$ and $h_t$ of the corresponding loops in $X$ and $Y$ .

Thus we obtain a bijection $\pi_1(X\times Y, (x_0,y_0))\approx \pi_1(X,x_0)\times \pi_1(Y,y_0)$ , $[f]\mapsto([g],[h])$ . This is clearly a group homomorphism, and hence an isomorphism.

Note: The condition that $X$ and $Y$ are path-connected implies that $\pi_1(X,x_0)=\pi_1(X)$ , $\pi_1(Y,y_0)=\pi_1(Y),\pi_1(X\times Y,(x_0,y_0))=\pi_1(X\times Y)$ .

Topological Monster: Alexander horned sphere

Very interesting object indeed. Also see this previous video on How to Unlock Interlocked Fingers Topologically?

The horned sphere, together with its inside, is a topological 3-ball, the Alexander horned ball, and so is simply connected; i.e., every loop can be shrunk to a point while staying inside. The exterior is not simply connected, unlike the exterior of the usual round sphere; a loop linking a torus in the above construction cannot be shrunk to a point without touching the horned sphere. (Wikipedia)

Hatcher 2.1.6

Compute the simplicial homology groups of the $\Delta$ -complex obtained from $n+1$ 2-simplices $\Delta_0^2, \dots, \Delta_n^2$ by identifying all three edges of $\Delta_0^2$ to a single edge, and for $i>0$ identifying the edges $[v_0,v_1]$ and $[v_1,v_2]$ of $\Delta_i^2$ to a single edge and the edge $[v_0,v_2]$ to the edge $[v_0,v_1]$ of $\Delta_{i-1}^2$ .

Wonderful Topology Notes for Beginners

Recently found a wonderful topology notes, suitable for beginners at: http://mathcircle.berkeley.edu/archivedocs/2010_2011/lectures/1011lecturespdf/bmc_topology_manifolds.pdf

It starts by pondering the shape of the earth, then generalizes to other surfaces. It also has a nice section on Fundamental Polygons and cutting and gluing, which was what I was looking for at first.

I have backed up a copy on Mathtuition88.com, in case the original site goes down in the future: bmc_topology_manifolds

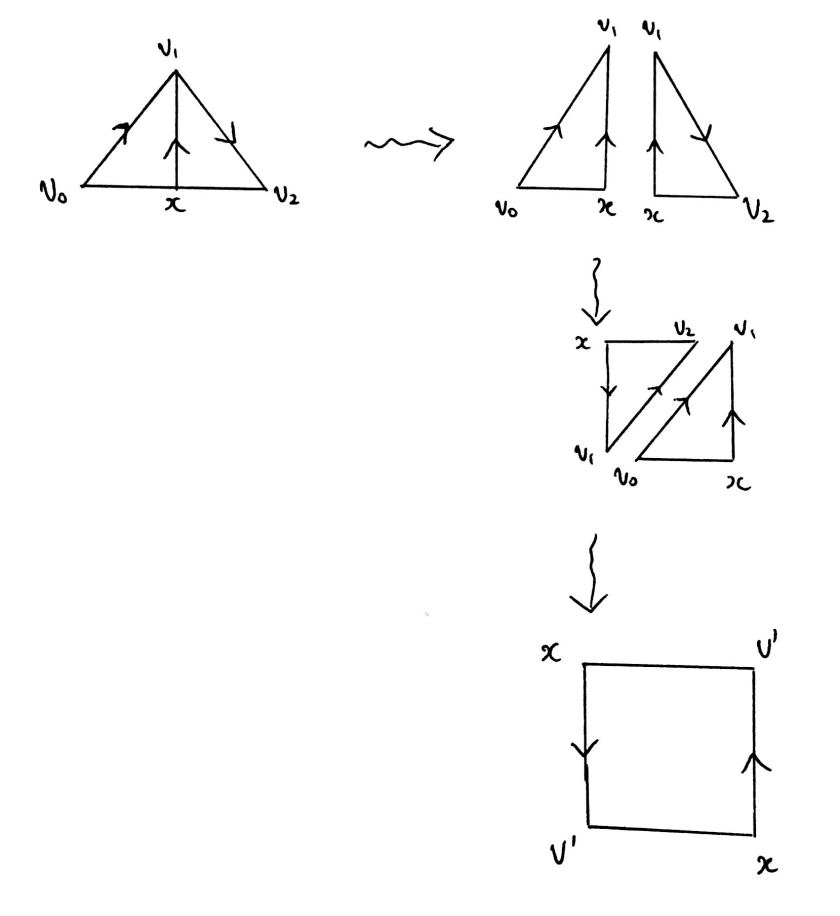
From Triangle to Mobius Strip

What familiar space is the quotient $\Delta$ -complex of a 2-simplex $[v_0,v_1,v_2]$ obtained by identifying the edges $[v_0,v_1]$ and $[v_1,v_2]$ , preserving the ordering of vertices?

This is a question from Hatcher. So if we “glue” two edges of the triangle together, preserving order, we get a Mobius Strip!

Covering map is an open map

We prove a lemma that the covering map $p:\tilde{X}\to X$ is an open map.

Let $U$ be open in $\tilde{X}$ . Let $y\in p(U)$ , then $y$ has an evenly covered open neighborhood $V$ , such that $p^{-1}(V)=\coprod A_i$ , where the $A_i$ are disjoint open sets in $\tilde{X}$ , and $p|_{A_i}:A_i\to V$ is a homeomorphism. $A_i\cap U$ is open in $\tilde{X}$ , and open in $A_i$ , so $p(A_i\cap U)$ is open in $U$ , thus open in $X$ .

There exists $x\in U$ such that $y=p(x)$ . Thus $x\in p^{-1}(y)\subseteq p^{-1}(V)$ so $x\in A_i$ for some $i$ . Thus $x\in A_i\cap U$ and thus $y\in p(A_i\cap U)\subseteq p(U)$ . This shows $y$ is an interior point of $p(U)$ . Hence $p(U)$ is open, thus $p$ is an open map.

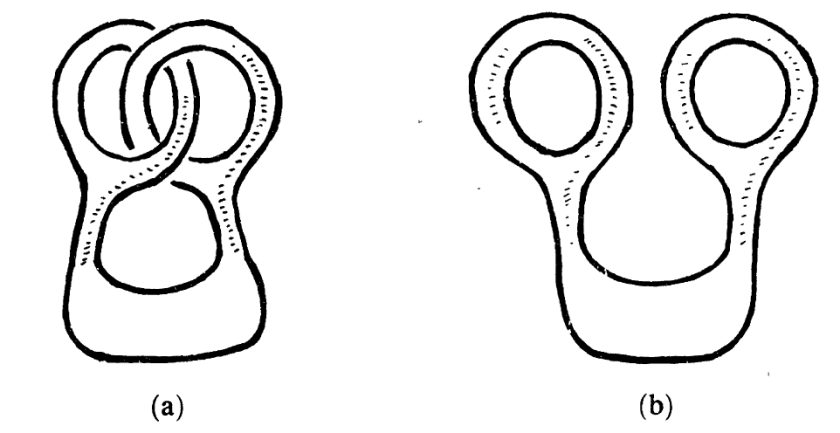
Topology Puzzle

Assume you are a superman who is very elastic, after making linked rings with your index fingers and thumbs, could you move your hands apart without separating the joined fingertips?

In other words, is it possible to go from (a) to (b) without “breaking” the figure above?

Figure taken from Intuitive Topology (Mathematical World, Vol 4).

The answer is yes!

This is an animation of the solution: https://vk.com/video-9666747_142799479

Topology book for General Audience

Previously I blogged about the book The Shape of Space, here is another book that is also about topology and suitable for a general audience (high school and above)!

Intuitive Topology (Mathematical World, Vol 4)

Effective Homotopy Method

The main idea of the effective homotopy method is the following: given some Kan simplicial sets $K_1,\dots,K_n$ , a topological constructor $\Phi$ produces a new simplicial set $K$ . If solutions for the homotopical problems of the spaces $K_1,\dots,K_n$ are known, then one should be able to build a solution for the homotopical problem of $K$ , and this construction would allow us to compute the homotopy groups $\pi_*(K)$ .

Representing map of x

Proposition:
(Representing map of $x$ ). Let $X$ be a simplicial set and let $x\in X_n$ . There exists a unique simplicial map $f_x:\Delta[n]\to X$ such that $f_x(\sigma_n)=x$ .
Proof:
Let $(i_0,i_1,\dots,i_k)\in\Delta[n]$ . $(i_0,i_1,\dots,i_k)$ can be written as iterated compositions of faces and degeneracies of $\sigma_n$ , i.e. $(i_0,i_1,\dots,i_k)=g\sigma_n$ where $g$ is an iterated composition of faces $(d_j)$ and degeneracies ( $s_j$ ). Then
$\begin{aligned} f_x(i_0,i_1,\dots,i_k)&=f_x(g\sigma_n)\\ &=gf_x(\sigma_n)\\ &=gx \end{aligned}$
This defines a unique simplicial map $f_x$ such that $f_x(\sigma_n)=x$ .

Minimal Simplicial Sets

Let $X$ be a space. We can have a fibrant simplicial set, namely the singular simplicial set $S_*(X)$ , where $S_n(x)$ is the set of all continuous maps from the $n$ -simplex to $X$ . However $S_*(X)$ seems too large as there are uncountably many elements in each $S_n(X)$ . On the other hand, we need the fibrant assumption to have simplicial homotopy groups. This means that the simplicial model for a given space cannot be too small. We wish to have a smallest fibrant simplicial set which will be the idea behind minimal simplicial sets.

Let $X$ be a fibrant simplicial set. For $x,y\in X_n$ we say that $x\simeq y$ if the representing maps $f_x$ and $f_y$ are homotopic relative to $\partial\Delta[n]$ .

A fibrant simplicial set is said to be minimal if it has the property that $x\simeq y$ implies $x=y$ .

Let $X$ be a fibrant simplicial set. $X$ is minimal iff for any $0\leq k\leq n+1$ , $v,w\in X_{n+1}$ such that $d_iv=d_iw$ for all $i\neq k$ implies $d_kv=d_kw$ .

In other words, it means that a fibrant simplicial set is minimal iff for any two elements with all faces but one the same, then the missed face must be the same.

Higher Homotopy Groups

We can generalise the idea to higher homotopy groups as follows.

Let $X$ be a pointed fibrant simplicial set. The fundamental group $\pi_n(X)$ is the quotient set of the spherical elements in $X_n$ subject to the relation generated by $x\sim x'$ if there exists $w\in X_{n+1}$ such that $d_0w=x$ , $d_1w=x'$ and $d_jw=*$ for $j>1$ .

The product structure in $\pi_n(X)$ is given by: $[x]+[x']=[d_1w]$ , where $w\in X_{n+1}$ such that $d_0w=x'$ , $d_2w=x$ and $d_jw=*$ for $j>2$ . Furthermore, the map $|\cdot|:\pi_n(X)\to\pi_n(|X|)$ preserves the product structure.

Associativity and Path Inverse for Fundamental Groupoids

Continued from Path product and fundamental groupoids

(Associativity). Let $X$ be a fibrant simplicial set and let $\lambda_1$ , $\lambda_2$ and $\lambda_3$ be paths in $X$ such that $\lambda_1(1)=\lambda_2(0)$ and $\lambda_2(1)=\lambda_3(0)$ . Then $(\lambda_1*\lambda_2)*\lambda_3\simeq\lambda_1*(\lambda_2*\lambda_3)\ \text{rel}\ \partial\Delta[1]$

Let $y\in Y_0$ be a point. Denote $\epsilon_y:X\to Y$ as the constant simplicial map $\epsilon(x)=s_0^n(y)$ for $x\in X_n$ .

(Path Inverse). Let $X$ be a fibrant simplicial set and let $\lambda$ be a path in $X$ . Then there exists a path $\lambda^{-1}$ such that $\lambda*\lambda^{-1}\simeq\epsilon_{\lambda(0)}\ \text{rel}\ \partial\Delta[1]$ .

Path product and fundamental groupoids

Let $\sigma_1=(0,1)\in\Delta[1]_1$ . A path is a simplicial map $\lambda:\Delta[1]\to X$ . Since $\text{Hom}(\Delta[1],X)\cong X_1$ , the paths are in one-to-one correspondence to the elements in $X_1$ via the function $\lambda\mapsto x_\lambda=\lambda(\sigma_1)$ . The initial point of $\lambda$ is $\lambda(0)=\lambda(d_1\sigma_1)=d_1x_\lambda\in X_0$ , and the end point of $\lambda$ is $\lambda(1)=\lambda(d_0\sigma_1)=d_0x_\lambda\in X_0$ .

Let $\lambda$ and $\mu$ be two paths such that $\lambda(1)=\mu(0)$ . Then $d_0x_\lambda=d_1x_\mu$ and thus the elements $x_0=x_\mu$ and $x_2=x_\lambda$ have matching faces (with respect to 1).

Homotopy Groups

Let $X$ be a pointed fibrant simplicial set. The homotopy group $\pi_n(X)$ , as a set, is defined by $\pi_n(X)=[S^n,X]$ , i.e. the set of the pointed homotopy classes of all pointed simplicial maps from $S^n$ to $X$ . $\pi_n(X)=\pi_n(|X|)$ as sets.

An element $x\in X_n$ is said to be spherical if $d_i x=*$ for all $0\leq i\leq n$ .

Given a spherical element $x\in X_n$ , then its representing map $f_x:\Delta[n]\to X$ factors through the simplicial quotient set $S^n=\Delta[n]/\partial\Delta[n]$ . Conversely, any simplicial map $f:S^n\to X$ gives a spherical element $f(\sigma_n)\in X_n$ , where $\sigma_n$ is the nondegenerate element in $S^n_n$ . This gives a one-to-one correspondence from the set of spherical elements in $X_n$ to the set of simplicial maps $S^n\to X$ .

Path product and fundamental groupoids
Let $\sigma_1=(0,1)\in\Delta[1]_1$ . A path is a simplicial map $\lambda:\Delta[1]\to X$ .

Geometrical Meaning of Matching Faces

Let $X$ be a simplicial set. The elements $x_0,\dots,x_{i-1},x_{i+1},\dots,x_n\in X_{n-1}$ are said to be matching faces with respect to $i$ if $d_jx_k=d_kx_{j+1}$ for $j\geq k$ and $k,j+1\neq i$ .

Geometrically, matching faces are faces that “match” along lower-dimensional faces. In other words, they are “adjacent”.

In the 2-simplex, let $x_0=v_1v_2$ , $x_1=v_0v_2$ , $x_2=v_0v_1$ . Then $x_0, x_2$ are matching faces with respect to 1, since $d_1x_0=v_1=d_0x_2$ .

In the 3-simplex, let $x_0=v_1v_2v_3$ , $x_1=v_0v_1v_2$ , $x_2=v_0v_1v_3$ , $x_3=v_0v_1v_2$ . Then $x_0$ , $x_2$ , $x_3$ are matching faces with respect to 1, since the following hold:
$\begin{aligned} d_1x_0&=v_1v_3=d_0x_2\\ d_2x_0&=v_1v_2=d_0x_3\\ d_2x_2&=v_0v_1=d_2x_3 \end{aligned}$

Fibrant Simplicial Set

Let $X$ be a simplicial set. Then $X$ is fibrant if and only if every simplicial map $f:\Lambda^i[n]\to X$ has an extension for each $i$ .

Assume that $X$ is fibrant. Let $f:\Lambda^i[n]\to X$ . The elements $f(d_0\sigma_n),f(d_1\sigma_n),\dots,f(d_{i-1}\sigma_n),f(d_{i+1}\sigma_n),\dots,f(d_n\sigma_n)$ are matching faces with respect to $i$ . This is because for $j\geq k$ and $k,j+1\neq i$ ,

$\begin{aligned} d_jf(d_k\sigma_n)&=f(d_jd_k\sigma_n)\\ &=f(d_kd_{j+1}\sigma_n)\\ &=d_kf(d_{j+1}\sigma_n) \end{aligned}$
Thus, since $X$ is fibrant, there exists an element $w\in X_n$ such that $d_jw=f(d_j\sigma_n)$ for $j\neq i$ . Then, the representing map $g=f_w:\Delta[n]\to X$ , $f_w(\sigma_n)=w$ , is an extension of $f$ .

Conversely let $x_0,\dots,x_{i-1},x_{i+1},\dots,x_n\in X_{n-1}$ be any elements that are matching faces with respect to $i$ . Then the representing maps $f_{x_j}:\Delta[n-1]\to X$ for $j\neq i$ defines a simplicial map $f:\Lambda^i [n]\to X$ such that the diagram

Screen Shot 2016-01-26 at 11.21.11 PM
commutes for each $j$ .

By the assumption, there exists an extension $g:\Delta[n]\to X$ such that $g|_{\Lambda^i[n]}=f$ . Let $w=g(\sigma_n)$ . Then $d_jw=d_jg(\sigma_n)=g(d_j\sigma_n)=f(d_j\sigma_n)=x_j$ for $j\neq i$ . Thus $X$ is fibrant.