This blog post is on Rouche’s Theorem and some applications, namely counting the number of zeroes in an annulus, and the fundamental theorem of algebra.
Rouche’s Theorem: Let  ,
,  be holomorphic inside and on a simple closed contour
be holomorphic inside and on a simple closed contour 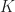 , such that
, such that  on
on 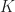 . Then
. Then 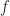 and
and 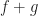 have the same number of zeroes (counting multiplicities) inside
have the same number of zeroes (counting multiplicities) inside 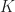 .
.
Rouche’s Theorem is useful for scenarios like this: Determine the number of zeroes, counting multiplicities, of the polynomial  in the annulus
in the annulus 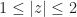 .
.
Solution:
Let 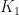 be the unit circle
be the unit circle  . We have
. We have

on 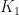 .
.
Since  has 2 zeroes in
has 2 zeroes in 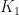 , therefore
, therefore 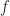 has 2 zeroes inside
has 2 zeroes inside 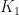 , by Rouche’s Theorem.
, by Rouche’s Theorem.
Let 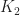 be the circle
be the circle 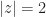
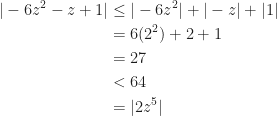
on 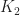 . Therefore
. Therefore 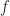 has 5 zeroes inside
has 5 zeroes inside 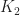 .
.
Therefore 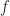 has 5-2=3 zeroes inside the annulus.
has 5-2=3 zeroes inside the annulus.
We do a computer check using Wolfram Alpha (http://www.wolframalpha.com/input/?i=2z%5E5-6z%5E2-z%2B1%3D0). The moduli of the five roots are (to 3 significant figures): 0.489, 0.335, 1.46, 1.45, 1.45. This confirms that 3 of the zeroes are in the given annulus.
Fundamental Theorem of Algebra Using Rouche’s Theorem
Rouche’s Theorem provides a rather short proof of the Fundamental Theorem of Algebra: Every degree n polynomial with complex coefficients has exactly n roots, counting multiplicities.
Proof: Let 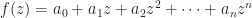 . Chose
. Chose  sufficiently large so that on the circle
sufficiently large so that on the circle 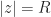 ,
,
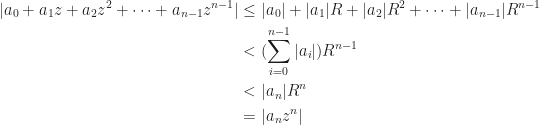
Since  has
has 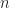 roots inside the circle,
roots inside the circle, 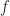 also has
also has 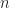 roots in the circle, by Rouche’s Theorem. Since
roots in the circle, by Rouche’s Theorem. Since 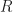 can be arbitrarily large, this proves the Fundamental Theorem of Algebra.
can be arbitrarily large, this proves the Fundamental Theorem of Algebra.
