Below is an excellent intuitive explanation (in Chinese) of the abstract concept Motif by Grothendieck:
Brief summary – Motif is the source of all “beautiful things” expressed in different forms.
Example : God created Natural Numbers (N), we express N in different forms: Binary (0, 1), Decimal (0, 1, 2 …9), Hexadecimal (0,1, 2…9, a, b, c, …f), etc. However, the “Motif” behind these forms is they all follow : 1) Commutative Law ; 2) Distributive Law.
Similarly, in Algebraic Geometry applying the cohomology from Algebraic Topology: étale cohomology, crystalline cohomology, de Rham cohomology are the different forms (~ Binary, Decimal, Hexadecimal), factored throught the common “Motif” of the Universal cohomology (~N).
[My Analogy in IT Language]:
Motif is like Interface or Generic, it spells out only the specification, leaving out the implementation (method) for actual classes / functions…







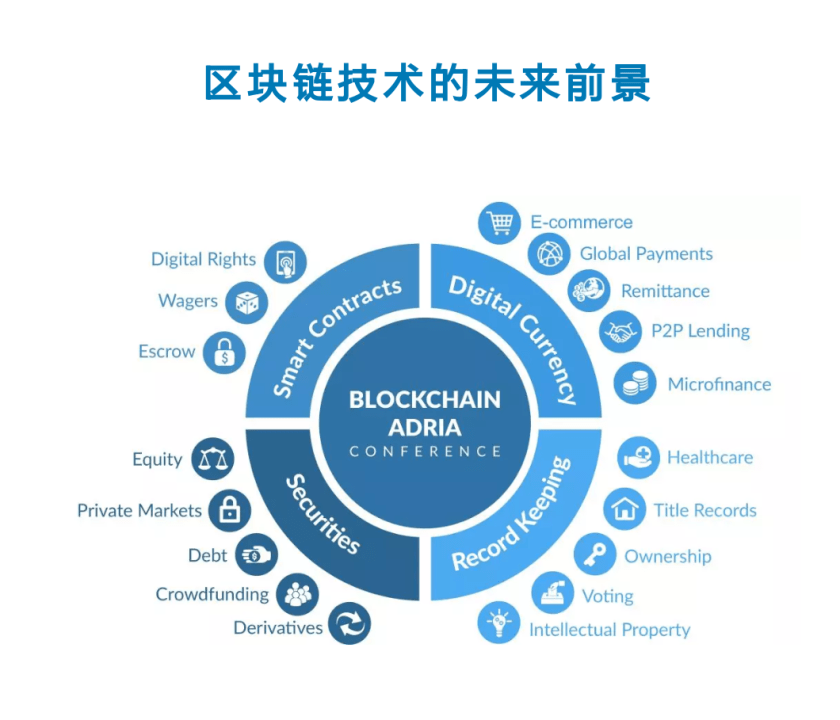
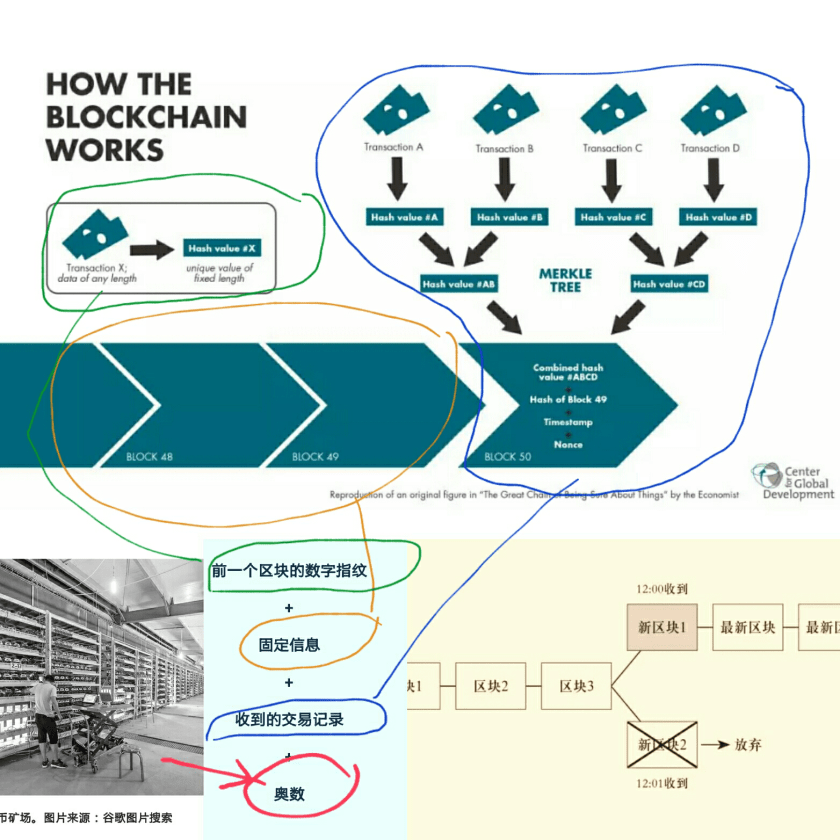






 1.2 Group of Non-Euclidean Motions:
1.2 Group of Non-Euclidean Motions:


 Key Words: 250 years anniversary
Key Words: 250 years anniversary




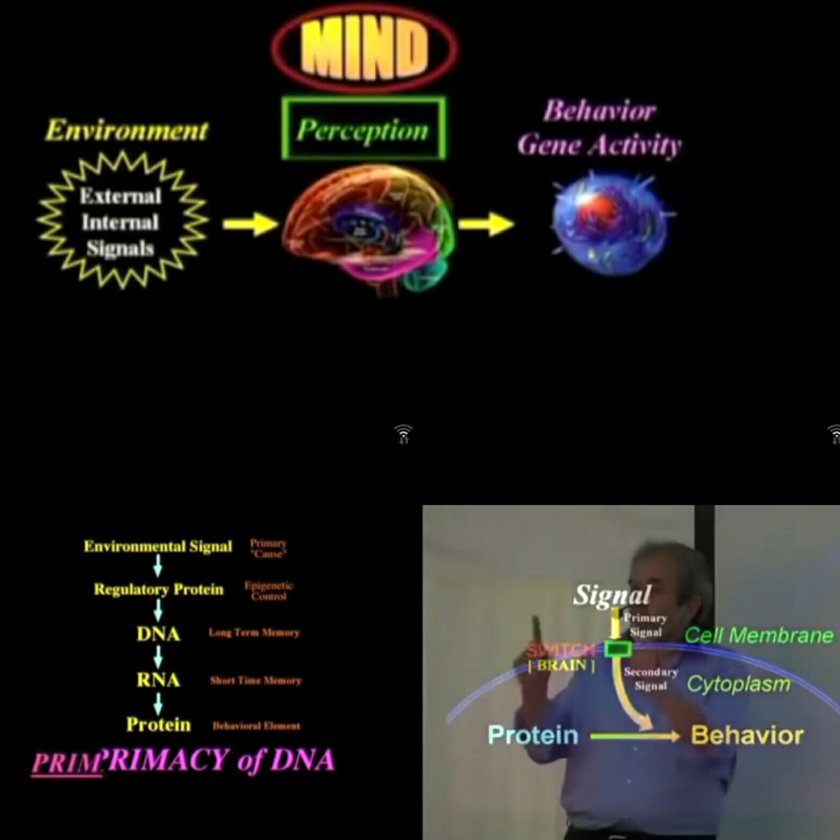
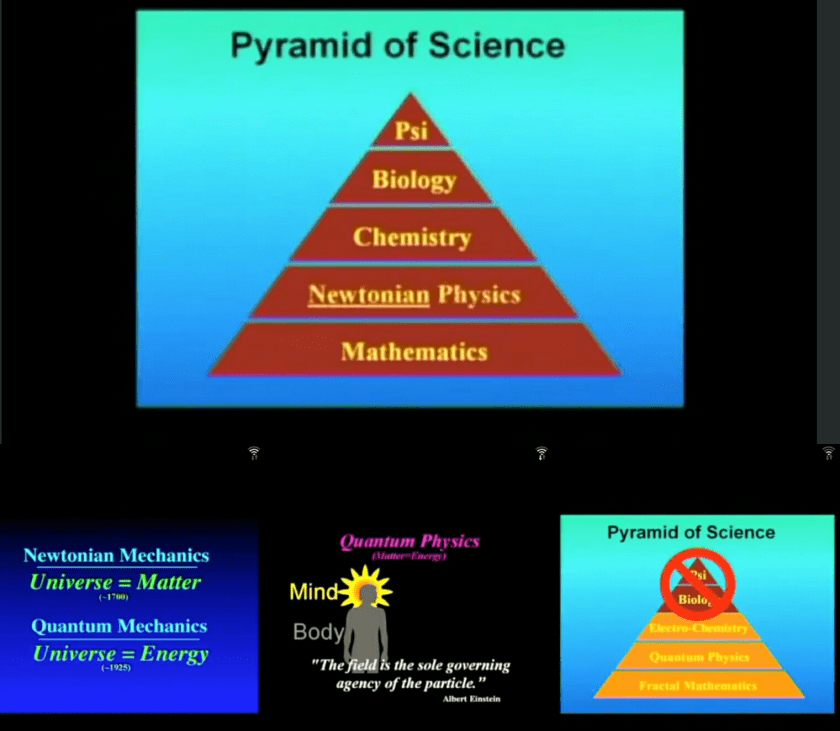 Energy = Field = 气 Chi / Qi
Energy = Field = 气 Chi / Qi














 Great Books Recommended –
Great Books Recommended – Note: Available at Singapore National…
Note: Available at Singapore National…


