This post will be a guide on how to calculate Homology Groups, focusing on the example of the Klein Bottle. Homology groups can be quite difficult to grasp (it took me quite a while to understand it). Hope this post will help readers to get the idea of Homology. Our reference book will be Hatcher’s Algebraic Topology (Chapter 2: Homology). I will elaborate further on the Hatcher’s excellent exposition on Homology.
This is also Exercise 5 in Chapter 2, Section 2.1 of Hatcher.
The first step to compute Homology Groups is to construct a 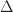 -complex of the Klein Bottle.
-complex of the Klein Bottle.

One thing to note for 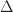 -complexes, is that the vertices cannot be ordered cyclically, as that would violate one of the requirements which is to preserve the order of the vertices.
-complexes, is that the vertices cannot be ordered cyclically, as that would violate one of the requirements which is to preserve the order of the vertices.
The key formula for Homology is:  .
.
We have  , the free group generated by the vertex
, the free group generated by the vertex  , because there is only one vertex!
, because there is only one vertex!
Next, we have  . Thus
. Thus  .
.
Therefore  .
.
Next, we have  .
.  ,
,  . To learn more about calculating
. To learn more about calculating  , check out the diagram on page 105 of Hatcher.
, check out the diagram on page 105 of Hatcher.
We then have  , where we got
, where we got  from adding the two previous generators
from adding the two previous generators  .
.
Thus  .
.
To intuitively understand the above working, we need to use the idea that elements in the quotient are “zero”. Hence  , implies that
, implies that  , thus
, thus  can be expressed as a linear combination of
can be expressed as a linear combination of  , thus is not a generator of
, thus is not a generator of 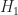 .
.  implies that
implies that  , which gives us the
, which gives us the  part.
part.
Finally we note that  , and also for
, and also for 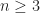 ,
,  since there are no simplices of dimension greater than or equal to 3. Thus, the second homology group onwards are all zero.
since there are no simplices of dimension greater than or equal to 3. Thus, the second homology group onwards are all zero.
In conclusion, we have 
is a space and
is a nonempty closed subspace that is a deformation retract of some neighborhood in
, then there is an exact sequence
is the inclusion
and
is the quotient map
.
and
for
.
take
so that
. The terms
in the long exact sequence are zero since
is contractible.
are isomorphisms for
and that
. Starting with
,
for
, the result follows by induction on
.


