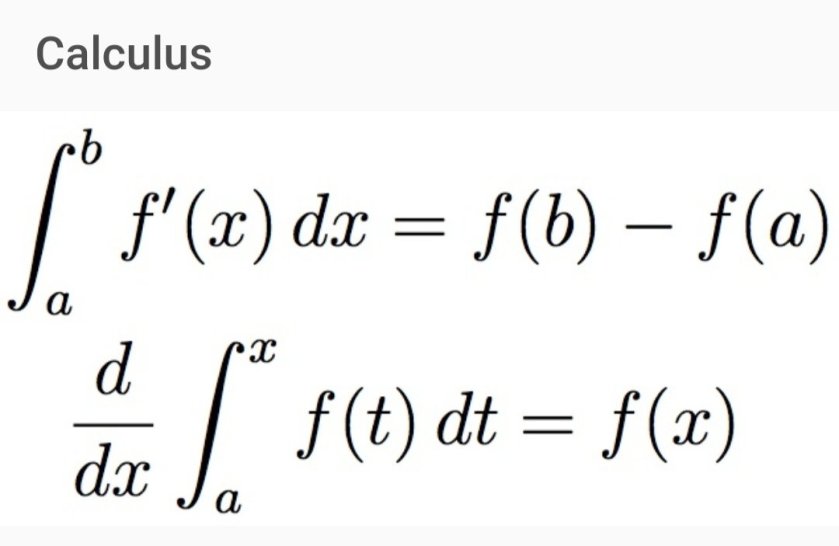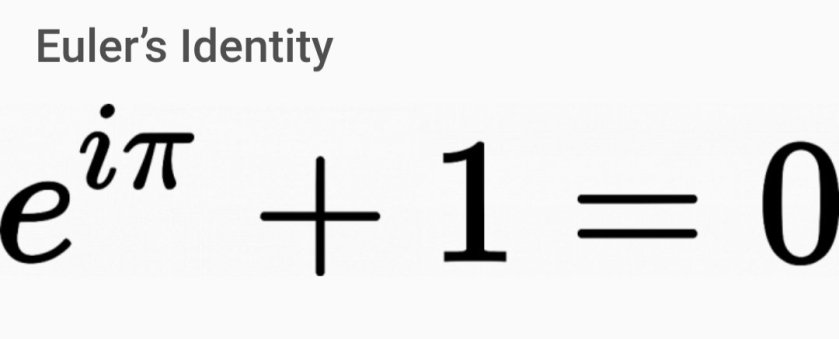Author: tomcircle
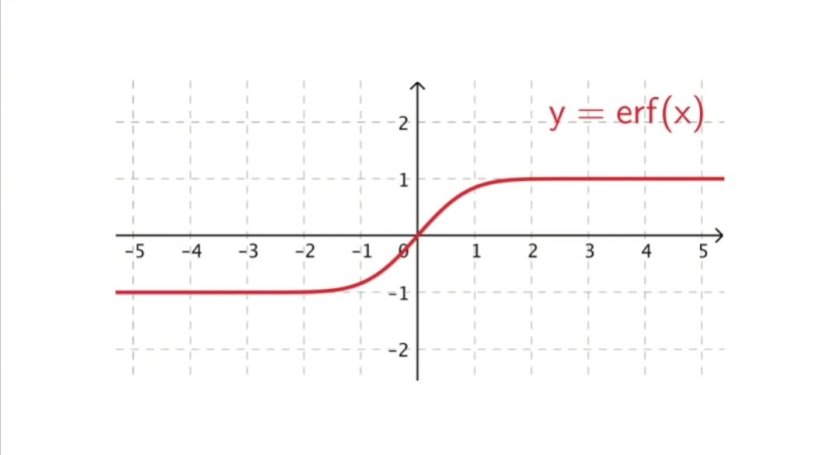
The Error Function & The Integral of e^(-x^2)
$latex boxed{ displaystyle erf(x) =
frac{2}{sqrt{pi}} int_{0}^{x} {e^{-{t}^2}dt}}&fg=aa0000&s=3
$

The Bell Curve:
$latex boxed{displaystyle y = e^{-x^2}}&fg=0000aa&s=3$
The most beautiful and important mathematical equations
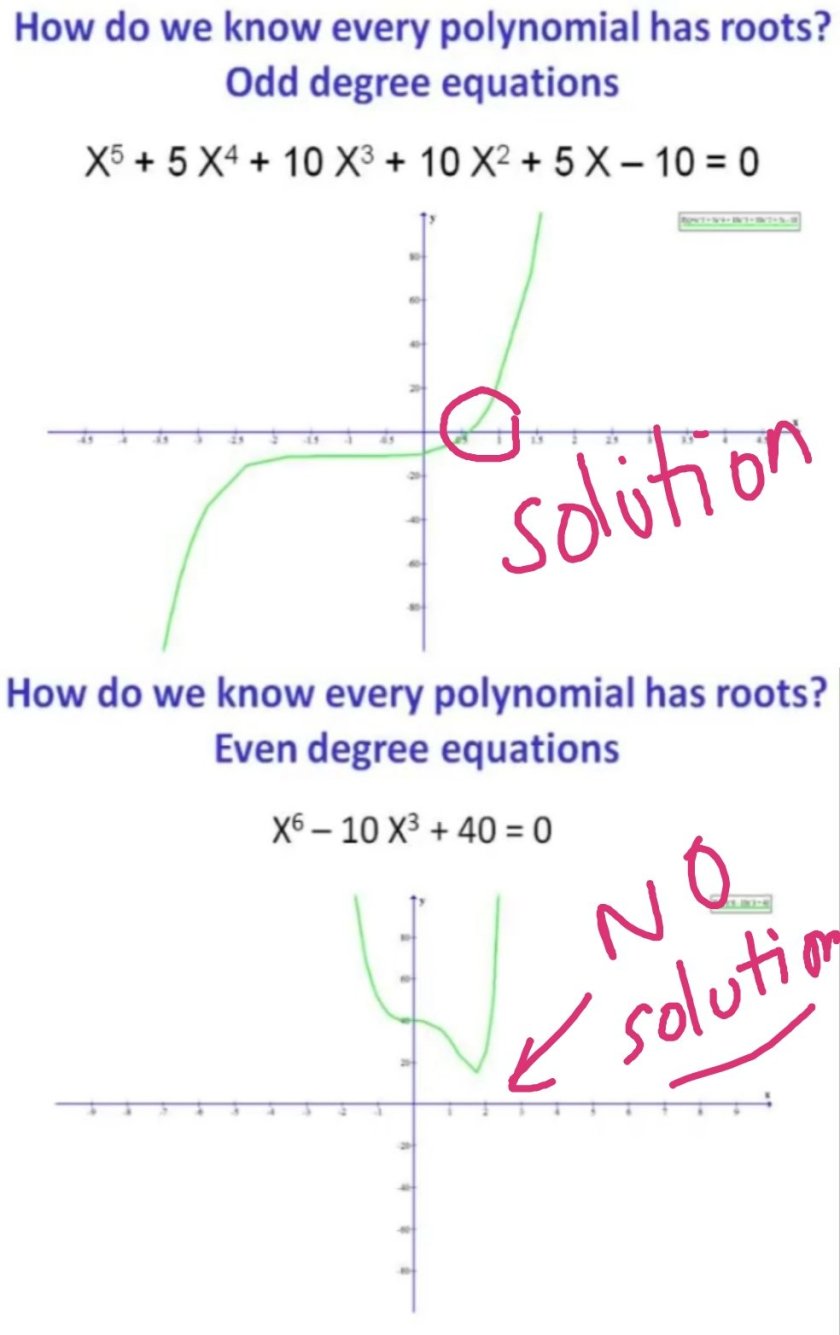
From Polynomial to Modern Algebra
13 classic mathematics books for lifelong learners
Out of 13 must-read Popular Math books, our Singapore National Library NLB has 6 which I borrowed and read: eg. “Prime Obsession” , “What is Mathematics” , etc.
Popular math books are better than the boring textbooks (Axiom – Theorem – Proof – Exercise). They are motivational, more concrete instead of abstract, philosophical analogy with the Nature (afterall, the math ideas derived from the universe, eg. Pi, e, golden ratio, infinity, limit, …), plus the historical background in which these math ideas were first discovered, and the beauty of these inter-connected ideas such as the Euler’s Identity:
$latex boxed{e^{i. pi} + 1 = 0}&fg=aa0000&s=3 $
“Proof from the Book” – the name “Book” (God’s Theorem Proof Book) is coined by Paul Erdos the Hungarian ‘vagabond’ (homeless, single, no nationality) mathematician, who had proven 1000+ theorems (some co-operated with his students). He said…
View original post 152 more words
Logic & Math (Set Theory)
Cambridge Prof Peter Smith:

You can download the book at the bottom link from the below web site.
https://boingboing.net/2018/12/26/beyond-a-equals-a.html/amp?from=singlemessage
Philosophy using Math – that is cool!

Set Theory is Philosophy, see this “Set Proofing Technique” taught in French Baccalaureate high school but Cambridge GCE A level ignores :
Prove : A = B
You need to prove 2 ways:
A ⊂ B
and
B ⊂ A
=> A = B
In the Bible 《John 14:11》
Jesus said to his disciples:
“Believe me when I say that I am in the Father and the Father is in me”.
Proof: Father (God) = Jesus
“Father in Me” :
<=>
Father ⊂ Jesus
and
“I am in the Father” :
<=>
Jesus ⊂ Father
Hence,
Jesus = Father (God)
[QED. ]
Merry Xmas! 圣诞快乐!
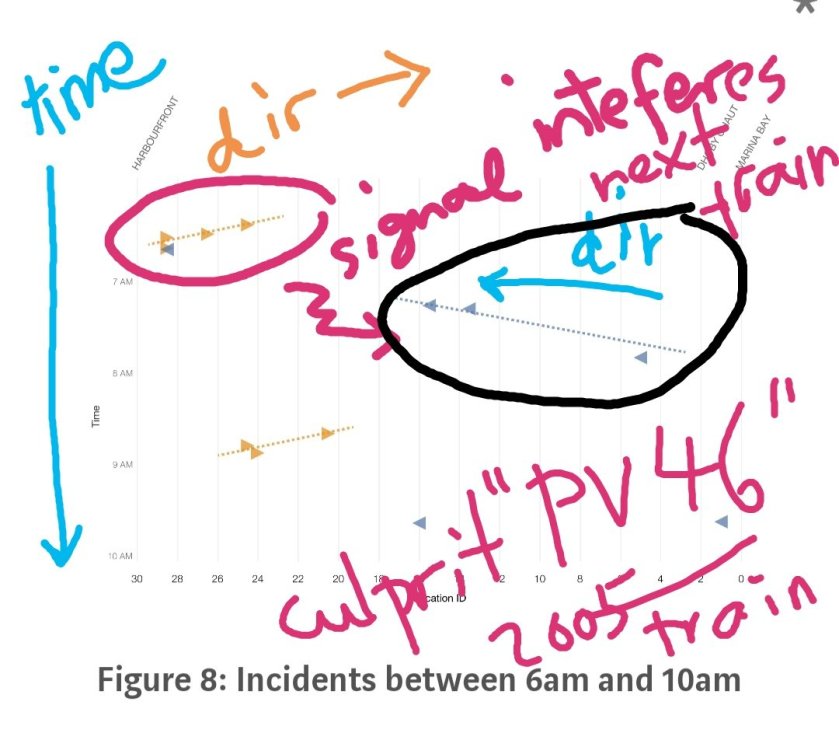
How Singapore Data Scientists caught the subway MRT “Circle line” rogue train
Quara: Strategy to teach yourself math from basic algebra to high level mathematics
If you had to teach yourself math from basic algebra to high level mathematics, what would be your strategy?
Chinese Primary School Math
As shown in the picture below, find the height of the table?
(No Algebraic equation please for Primary School Math).
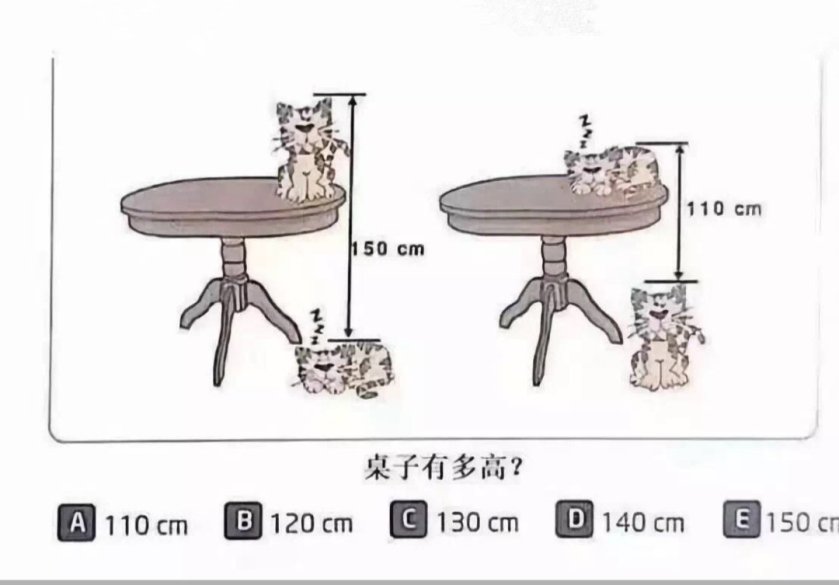
Answer: [hint = 130 cm]
Try yourself before scrolling down.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
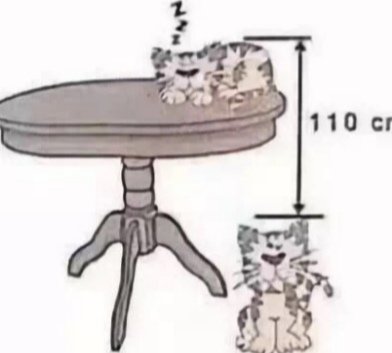
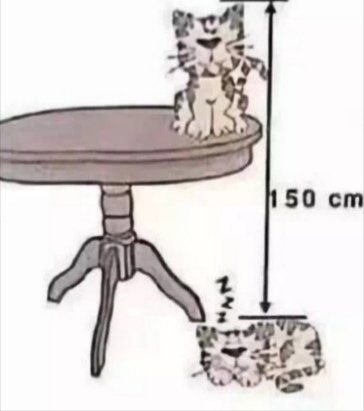
假设把右图桌子摞在左边桌子上,那么地面上趴着的猫到两个桌子上趴着的猫距离是260cm,那么两个桌子的高度是260cm,所以一个桌子高130cm.
The 2 sleeping cats and 2 sitting cats cancel out, left 260 (= 110+150) for the 2x Table Heights.
1 Table Height = 260/2 = 130 cm.
How you pronounce German Mathematician’s Names ( and Physicists )
Germany produced many Mathematicians and Physicists who succeeded the 18 CE Newtonian England, and the 19CE Napoleonic France before WW2, after which the Americans (mostly the Jewish German immigrants) take over till now.
German names are difficult to pronounce for foreigners.
Libniz,
Euler,
Einstein,
Noether,
Gauss,
Dedekind,
Riemann,
Cantor,
etc.
For due respect, please learn to pronounce their German name correctly.
Euler’s and Fermat’s last theorems, the Simpsons and CDC6600
I am a fan of Fermat, not only because my university Alma Mater was in his hometown Toulouse (France) named after him “Lycée Pierre de Fermat (Classe Préparatoire Aux Grandes Ecoles) ” , but also the “Fermat’s Last Theorem” (FLT) has fascinated for 350 years all great Mathematicians including Euler, Gauss,… until 1993 finally proved by the Cambridge Professor Andrew Wiles. Another “Fermat’s Little Theorem” is applied in computer Cryptography .

Below is the explanation of (n = 4) case proved by Fermat and the latest proof by contradiction.
Euler Conjecture: extends FLT to 4 or more integers if FLT still holds? (a contradiction found).

Simpsons “Fool” Equality: Proof by contradiction (odd = even)
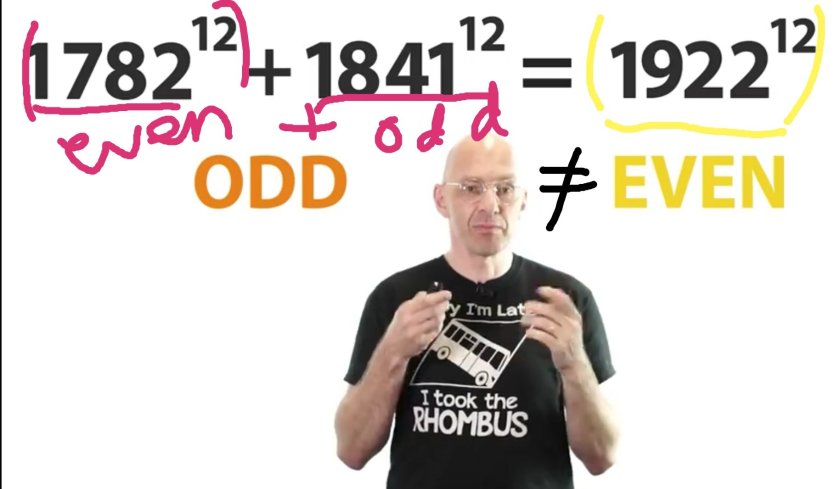

Proof of FLT by Andrew Wiles (1993):

The proof by Contradiction of FLT (n=4) is in Part 2 of the video after 20:30 mins (Warning: a bit heavy)
Improper Integral vs. Infinite Series
$latex displaystyle int_{2}^{infty}{frac{1}{x^{2} – 1}dx} =boxed{ ln {3}}$
$latex displaystyle sum_{n=2}^{infty}{frac{1}{n^{2} – 1}} = boxed{frac{3 } {2 }} $
To test if the infinite series
$latex displaystyle sum_{n=2}^{infty}{frac{1}{n^{2} – 1}} $ converges, provided it is
- positive &
- decreasing function
you can convert it to $latex displaystyle int_{2}^{infty}{frac{1}{x^{2} – 1}dx} $
(although they converge to different values.)
Integration by parts, DI method
This DI method is American way, better than the UK Cambridge O level technique.
(Traditional Method learnt at O-Level) Integration by Parts:

NEW Technique taught by this UC-Berkley Chinese Mathematician: “DI” Method
First Stop: “D column at…“

2nd Stop:

3rd Stop:
$latex displaystyle int {e^{x}}sin {x} dx$

View original post 1 more word
The Best Movies For Mathematicians
Analysis by Timothy Gowers
Why easy analysis problems are easy
by Timothy Gowers (UK, Fields Medal 1998)
Timothy Gowers is teaching in Cambridge, he wrote the thick volume of “Princeton Math Encyclopedia.”
He is a very good mathematician, who likes to explain simple fundamental Math questions (like why 2+2=4, multiplication is commutative,…), in the process making abstract math simple to understand.
“If you have recently met epsilons and deltas for the first time, then you may find the problems you are asked to solve on examples sheets very hard. On the other hand, you will notice that your lecturers, supervisors etc. do not find them hard at all. Why is this? ” Read on …
https://www.dpmms.cam.ac.uk/~wtg10/autoanalysis.html
Below is my attempt to rewrite the Example 1 with Latex epsilon-delta notation for easy reading.
Example 1.
I wish to prove that the sequence (1,0,1,0,1,0,…) does not converge.
$latex text{Let me set the sequence }
View original post 174 more words
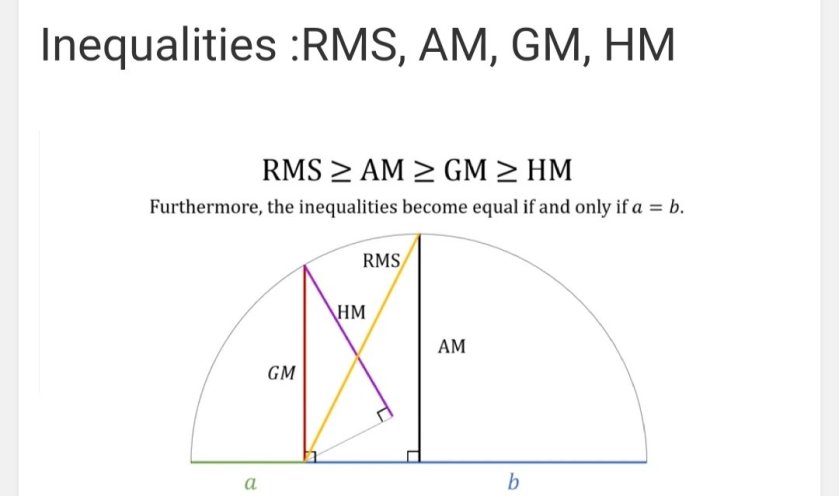
Inequalities : RMS, AM, GM, HM
Integral of x^x from 0 to 1
$latex boxed {displaystyleint_{0}^{1}{x^{x}dx }= frac {1}{1^1} – frac {1}{2^2} +frac {1}{3^3} – frac {1}{4^4} + frac {1}{5^5} +…}$
$latex boxed {displaystyleint_{0}^{1}{x^{-x}dx }= frac {1}{1^1} +frac {1}{2^2} +frac {1}{3^3} + frac {1}{4^4} + frac {1}{5^5} + …}$
My favorite Fermat Little Theorem with Pascal Triangle
Fermat Little Theorem: For any prime integer p, any integer m
$latex boxed {m^{p} equiv m mod p} &s=3$
When m = 2,
$latex boxed{2^{p} equiv 2 mod p}&fg=aa0000$
Note: 九章算数 Fermat Little Theorem (m=2)
Pascal Triangle (1653 AD France )= (杨辉三角 1238 AD – 1298 AD)
$latex 1 : 1 implies sum = 2 = 2^1 equiv 2 mod 1$
$latex 1: 2 :1implies sum = 4 = 2^2 equiv 2 mod 2 ;(equiv 0 mod 2)$
$latex 1 :3 :3 :1 implies sum = 8= 2^3 equiv 2 mod 3$
1 4 6 4 1 => sum = 16= 2^4 (4 is non-prime)
$latex 1 :5 :10: 10: 5: 1 implies sum = 32= 2^5 equiv 2 mod 5$

[PODCAST]
https://kpknudson.com/my-favorite-theorem/2017/9/13/episode-4-jordan-ellenberg
Math Challenge: Teaching Subject

[Hint] : Assume 3 cases, then by Elimination using Mr Brown’s hint (somethingS right, somethingS wrong)
Math Paradox : Toroflux
What is Riemann’s Hypothesis ?
[中文]历史 History:
Sir Atiyah Proof on 2018 September : (5 Pages PDF download here)
https://drive.google.com/file/d/17NBICP6OcUSucrXKNWvzLmrQpfUrEKuY/view
Bigger Lecture Notes video (at 34 mins, inspired in Singapore)
Analytic function: preserve angle after transformation

The most addictive theorem in Applied mathematics
What is your favorite theorem ?
I have 2 theorems which trigger my love of Math :
- Chinese Remainder Theorem:韩信点兵, named after a 200 BCE Han dynasty genius general Han Xin (韩信) who applied this modern “Modular Arithmetic” in battle fields.
- Fermat’s Last Theorem:The Math “prank” initiated by the 17CE amateur Mathematician Pierre de Fermat kept the world busy for 380 years until 1974 proved by Andrew Wiles.
Note 1: Lycée Pierre de Fermat (Classe Préparatoire) happens to be my alma mater named after this great Mathematician born in the same southern France “Airbus City” Toulouse.
Note 2: His another Fermat’s Little Theorem is used in modern computer cryptography.
WiFi Password = Integral Answer
China Nanjing Aviation University set the WiFi password as the answer of this integral (first 6 digits).
Can you solve it?
 Answer : Break the integral (I) into 2 parts:
Answer : Break the integral (I) into 2 parts:
I = A(x) + B(x)
$latex A(x) = int_{-2 }^ {2} x^{3}. cos (x/2).sqrt{4-x^2}dx$
$latex B(x) = int_{-2 }^ {2} 1/2.sqrt{4-x^2}dx$
A(x) = – A(-x) => Odd function
=> A =… since its area canceled out over [-2, 2]
B(x) = B(-x) => Even function
$latex implies B(x) = 2.int_{0 }^ {2} 1/2.sqrt{4 – x^2}dx$
$latex implies B(x) = int_{0 }^ {2} sqrt{4 – x^2}dx$
Let x = 2 sin t => dx = 2 cos t. dt
x = 2 = 2 sin t => sin t = 1 => t = π/2
x = 0 = 2 sin t => sin t = 0 => t =…
$latex B(x) = int_{0 }^ {pi/2} sqrt{4 – 4.sin^{2} {t}…
View original post 96 more words
[Quora] Common Core Math
Why did the approach to mathematics change with Common Core, rather than providing more structure to how it was previously taught? by Peter Kruger

Spot The Mistake?
Math is rigor. Where went wrong?
Solve:
$latex displaystyle {Bigl(frac{2}{3}Bigr)} ^{x} = {Bigl(frac{3}{2}Bigr)}^{3}$
$latex implies displaystyle frac {2^{x}} {3^{x}} = frac {3^{3}} {2^{3}}$
$latex implies displaystyle{2^{3}}. {2^{x}} ={3^{3}}. {3^{x}}$
$latex implies displaystyle2^{3+x} =3^{3+x}$
Since the exponents (3+x) on both sides are equal,
=> 2 = 3
153 St. Peter Fish
Bible Math: 153 St. Peter Fish
[John 21:3-11]
3 So they went out and got into the boat, but that night they caught nothing.
6 He said, “Throw your net on the right side of the boat and you will find some.” When they did, they were unable to haul the net in because of the large number of fish... It was full of large fish, 153, but even with so many the net was not torn.
1) 153= 1! + 2! + 3! + 4! + 5! = (1+2+6+24+120)
2) $latex 1^3+5^3 +3^3$ = 1 + 125 + 27 = 153
3) Take any multiple of 3, e.g. 78
-> $latex 7^3+8^3$ = 855
-> $latex 8^3+5^3+5^3$ = 762
762 -> 567 ->684 ->792 ->1080 ->513 ->153 (Always!)
French Baccalaureate Math
Below are two French Baccalaureate Math textbooks (Volume 1 & 2) for Grade 12th (or Junior College Year 2, GCE A Level, Lycée: Terminale C) students in the late 1970s.
There was a strong Bourbaki style of influence in this Math teaching, which was later criticized as being too abstract and less applied for 18-year-old students.
Nevertheless, the syllabus proved to be excellent for those Math-inclined young minds who later entered the special 2-year Classe Préparatoire aux Grandes Ecoles – Preparatory class (equivalent to Bachelor of Science) for graduate schools in crème de la crème top universities (Grandes Écoles ) such as Ecole Normale Supérieure or Ecole Polytechnique , where the solid Preparatory Math trainings (Maths Supérieures, Maths Spéciales) are extremely rigorous and high standard, incubating most of the French great mathematicians, Fields Medalists and Nobel Prize Scientists.
Voici les 2 tomes de Mathematiques Terminales C et E
View original post 303 more words
Singapore PSLE Math baffled Anxious Parents
One afternoon 5 friends rented 3 bikes from 5 p.m. to 6:30 p.m. and took turns to ride on them. At any time, 3 of them cycled while the other 2 friends rested.
If each of them had the same amount of cycling time, how many minutes did each person ride on a bike?
Note: PSLE (Primary Schools Leaving Exams) is the Singapore National Exams for all 12 year-old pupils at Primary 6 year end. The result of which will determine which secondary school the pupil is qualified to enter the following year. Math subject, besides Science, English and mother tongue (Chinese or Malay or Tamil) are tested in PSLE.
[Answer] Try before you scroll down below ….
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
View original post 97 more words
The Universal Pattern Popping Up in Math, Physics and Biology
 Key Points:
Key Points:
- Bus Waiting Time Pattern
- Biology Chicken eyes
- Physics: Random matrix / Eigenvalues / Riemann Zeta-function for Prime Numbers
- Universal Pattern: Normal Distribution Curve
Nearest Neigbour Problem – Universal Method to Sort Complex Information Found
Key Points:
- Normed Distance: Euclidean
- Expander Graph
https://www.quantamagazine.org/universal-method-to-sort-complex-information-found-20180813/

Category Theory III for Programmers (Parts 1 & 2)
The most interesting “Category Theory” (范畴论) for Programmers course III by Dr. Bartosz Milewski , a follow-up of last year’s course II.
Prerequisites:
- Fundamental of Category Theory: Functor, Natural Transformation, etc. (Course II Series)
- (Nice to have) : Basic Haskell Functional Programming Language. (Quick Haskell Tutorial)
1.1: Overview Part 1
Category Theory (CT) = Summary ofALL Mathematics
Functional Programming = Application of CT
Philosophical Background:
- Math originated 3,000 years ago in Geometry by Greek Euclid with Axioms and deductive (演译) Proof-drivenLogic.
- Geometry = Geo (Earth) + Metry (Measurement).
- Math evolved from 2-dimensional Euclidean Geometry through 17 CE French Descartes’s Cartesian Geometry using the 13CE Arabic invention “Algebra” in Equations of n dimensions: $latex (x_1, x_2,…, x_n) $, $latex (y_1, y_2,…, y_n) $
- Use of Algebra: 1) Evaluation of algebraic equations (in CT: “Functor”) ; 2) Manipulation. eg. Substitution (in CT :…
View original post 194 more words
Programming is Math Proof: Structured Programming
Keywords:
- Dijkstra, Edge Wyber (born 1930 Rotterdam)
- Goto is harmful
- Structures: sequence, selection, iteration
Three Programming Paradigms:
1. Structured Programming (1968 Dijkstra)
- Impose discipline on direct transfer of control aka “Goto“.
- “If/ then /else, do/while” control structures are structured.
2. Object-Oriented ‘OO’ (1966 Ole Johan Dahl & Kristen Nygaard)
- Impose discipline on Indirect transfer of control (polymorphism, ‘constructor‘ function of class, it’s local variables = instance variables).
OO = Combination of Data & Function.
3. Functional Programming (1958 John McCarthy’s LISP language, based on Math “Lambda Calculus” from Alonzo Church 1936).
- Impose discipline upon assignment (side effect, immutability of data, Referential Transparency).
4. Any more ?
All Programs can be constructed from just 3 structures (Böhm and Jacopini, 1966):
Sequence / Selection / Iteration.
Dijkstra’s Math Proofs for:
1. Sequence – by simple enumeration.
- Math Technique: trace the inputs…
View original post 72 more words
18个量子比特纠缠是什么?量子计算机为何如此强大?量子的纠缠态与叠加态
Thd World’s first 18-Qbit Quantum Computing by the young Chinese scientist Prof Pan (潘).
Lambda Calculus – The Math Behind Functional Programming
Functional Programming (FP) Languages : Lisp, Haskell, Scala, Kotlin, etc.
Other non-FP influenced by Lambda Calculus: Python, Ruby, Javascript, Java 8, C++
Inventor of Lambda Calculus : Alonzo Church (1903 – 1995), whose student in Princeton University (1936-1938) was Alan Turing (The Father of Artificial Intelligence).
Lambda Calculus is not : another Differential Calculus !
Note: Calculus has a meaning of manipulating symbolic expressions : either in functions (differentiation, integration) or computations.
Lambda Calculus is almost programming!
I. Syntax of Lambda Calculus: $latex boxed {lambda text { param . body }}&fg=aa0000&s=3$
eg. $latex lambda : x : . : x + 1 $
Notice: it has only one parameter “x”.
- Function definition: $latex lambda $
- Identifier reference: $latex x $
- Function application: $latex x + 1 $
II. Currying 柯里化 : (named after Haskell Curry ) for multiple parameters.
eg. $latex lambda : x : …
View original post 358 more words
How Piano Lessons May Improve Language Learning for Kids | Time
Music => Language => Abstractness (Abstract Mathematics, Advanced Physics), these 3 faculties reside on the same (right) part of our brain., the earlier a kid develops it through music education (piano, violin or any instrument) the better.
Infinite Cake
The Big Internet Math-Off, Round 1 – James Tanton v Nira Chamberlain | The Aperiodical
http://aperiodical.com/2018/07/the-big-internet-math-off-round-1-james-tanton-v-nira-chamberlain/
Celebrates Mathematician Gottfried Wilhelm Leibniz’s 372nd Birthday
My favorite mathematician is German Leibniz, who co-invented Calculus with Newton.
Today we thank Leibniz for his elegant Calculus symbols:
$latex boxed {frac{dy}{dx}}&s=3&fg=aa0000$
$latex boxed{int_{0}^{infty}x^{n}e^{-x}dx}&s=3&fg=aa0000$
Leibniz also invented 01 binary algebra, which he later found it was already in the 3,000-year-old Chinese “Yin-Yang” (阴阳 八卦), so impressed that he recommended to the most powerful western (French) king Louis XIV (14th) to use Chinese as the Universal Language of the world.
The rich Newton sued Leibniz for plagiarism of Calculus, until Leibniz died poor in bankruptcy, buried in a common unknown grave.
The war between Newton & Leibniz extended & lasted 100 years between UK Math Community and Continental Europe Math Community. As a result UK lost its math leadership after Newton, France (Lagrange, Fourier, Cauchy, Galois… ) followed by Germany (Felix Klein, Gauss, Hilbert, Riemann …) took over as the world…
View original post 27 more words
困扰了人类358年 费马大定理 Fermat’s Last Theorem
Keywords:
- Fermat’s Last Theorem (FLT):$latex boxed {x^{n} +y^{n} = z^{n} ; ; forall n >2 }&s=3&fg=aa0000$
- Pierre de Fermat (France 17CE): FLT Conjecture or Prank ?
- Euler (n= 3)
- Taniyama-Shimura-Weil Conjecture: Modular Form = Elliptic Curve
- Galois Group Symmetry
- Andrew Wiles (UK Cambridge 1994): (Modular Form = Elliptic Curve) = FLT (q.e.d.)
Notes: Do not confuse Prof Andrew Wiles (proved FLT) with (French/American) Prof André Weil (Founder of Bourbaki School of Modern Math in POST-WW2 universities worldwide) who proved (4) laying the ground work for FLT.
How Abstract Math Can Analyze Social Injustice
Science Friday: How Abstract Math Can Analyze Social Injustice.
Dr. Eugenia Cheng
 https://www.sciencefriday.com/segments/how-abstract-math-can-analyze-social-injustice/
https://www.sciencefriday.com/segments/how-abstract-math-can-analyze-social-injustice/
[Sound]:
https://m.soundcloud.com/scifri/how-abstract-math-can-analyze-social-injustice
 Interview: Yoneda Lemma
Interview: Yoneda Lemma

Worldcup Math Analysis : Korea vs Germany (2:0)
Football played with Math strategy !
Worldcup 2018
Surprising Result:
World No.1 (Germany) Lost to World No.59 (Korea) – why ?
Reason: Math !
For weak Korea to win, the best strategy is to keep the goals number as low as possible with strongest defence.
Note : 2017 International Math Olympiad (IMO) World Champion Team was Korea.

The actual Game proved the Korean “Math” strategy was right: (2:0)
The Software War : Object-Oriented Programming (OOP) vs Functional Programming (FP)
The “war” of OOP vs FP is akin to Applied Math vs Pure Math.
The formers (OOP & Applied Math) are not “rigourous” but practical, compared to the laters (FP & Pure Math) which are elegant but too abstract for popular usage.
OOP: SmallTalk and its followers – C++, C#, Objective-C, Java…
FP: LISP and its followers – Haskell, Clojure, …
The “hybrid” (OOP&FP): Scala, Kotlin (Google: Java ‘cousin’), Swift (Apple: Objective -C ‘cousin’), F# (MicroSoft)
The “cons” of OOP, which are bad for concurrency / parallel computing in multi-cored CPU:
- State changed
- Side-effect
- Mutability of data
- Polymorphism
 https://blog.cleancoder.com/uncle-bob/2014/11/24/FPvsOO.html
https://blog.cleancoder.com/uncle-bob/2014/11/24/FPvsOO.html
Group is Symmetry
Landau’s book “Symmetry” explains it as follow:
Automorphism = Congruence= 叠合 has
1). Proper 真叠合 (symmetry: left= left, right = right)
2). Improper 非真叠合 (non-symmetry: reflection: left changed to right, vice-versa).
Congruence => preserve size / length
=> Movement 运动 (translation 平移, rotation about O )
= Proper congruence (Symmetry)
In Space S, the Automorphism that preserves the structure of S forms a Group Aut(G).
=> Group Aut(G) describes the Symmetry of Space S.
Hence Group is the language to describe Symmetry.
Noether Theorem: Symmetry
Symmetry (hence Group) explains :
1. Conservation of Energy;
2. Conservation of Angular Momentum;
3. Periodic Table;
4. Laws of Thermodynamic.
Emmy Noether Theorem (1918): Conservation Laws owes to Symmetry :
1. In Linear motion
=> Conservation of Momentum
2. In Angular movement
=> Conservation of Angular Momentum
3. In Time
=> Conservation of Energy
Mathematician Emmy Noether changed the face of physics
Why do the French excel in maths ?
It is not only owed to the Ecole Normale Superieure where the 11 Fields medalists were educated, but the prominent “Math Culture” in French society.
This is similar to the International Math Olympiad (IMO) “craze” in China since 1980s till today, where the parents send their primary school kids to drill in IMO boot- camps, because that is a “direct-entry” gateway to enter top university, bypassing the highly competitive “Gao-kao” 高考 (High-school College Entrance Exams for 500,000 places among 7 million students each year).
https://www.theguardian.com/world/2012/may/31/europa-french-maths-ecoles-normales-superieures
Quora: read how this middle-age (48) French recounts his “French Math” education since 6 to 15 years old:
The curriculum was designed in the late 60s in part by a group of real mathematicians, the Bourbaki. It was very abstract. I learned about basic set theory when I was 6. I did learn about the basic operators but not before I was able to perform…
View original post 97 more words
Chinese Remainder Theorem 中国剩余定理
中国剩余定理CRT (Chinese Remainder Theorem)
X ≡ 2 (mod 3)
X ≡ 3 (mod 5)
X ≡ 2 (mod 7)
Solve X?
明. 程大位 “算法统宗” (1593)
3人同行70稀
5树梅花21支
7子团圆半个月(15)
除百零五(105)便得知
Let remainders:
$Latex r_3=2, r_5=3, r_7=2$
$Latex r= r_3.70+ r_5.21 + r_7.15 (mod 3.5.7)$
r= 2.70 +3.21 +2.15 (mod 105)
r= 140 +63 +30 (mod 105)
r= 233 (mod 105)
$latex r= 23 = x_{min}$
or X= 23 +105Z (23 + multiples of 105)
——————————————-
CRT: Why 3:70, 5:21, 7:15
X ≡ 2 (mod 3)
X ≡ 3 (mod 5)
X ≡ 2 (mod 7)
1) Find A such that
A ≡ 1 (mod 3)
A ≡ 0 (mod 5)
A ≡ 0 (mod 7)
=> 5|A, 7|A => 35 |A
View original post 181 more words
韩信点兵 (中国剩余定理)
Chinese Remainder Theorem (CRT): 韩信点兵 (中国剩余定理)
南北朝 《孙子算经》(4 AD)
《孙子算经》中的鸡兔同笼问题
Yijing & Orchestra Conductor
Problem:
The Orchestra conductor has been asked to conduct a series of concert for 2 consecutive months.
The Orchestra has to play few pieces of classical music with the following conditions requested by the organising committee:
1) Play at least 1 piece of music a day;
2) Avoid playing exactly the same music in 2 consecutive days (although partially is allowed)
3) Due to resource constraint, it is impossible to play all pieces of music within a single day.
Question:
At least how many (N) pieces of music the conductor has to prepare in order to fulfill these conditions?
Solution:
Using Yijing (易经)notation:
* a piece of music being played in a day is denoted by
__ (solid line);
while not being played is denoted by
– – (broken line)
* 2 consecutive months in any year have maximum 62 (= 31+31) days.
* A bagua (8…
View original post 141 more words