Recently, the Singapore Haze is getting quite bad, crossing the 200 PSI Mark on several occasions. Do consider purchasing a Air Purifier, or some N95 Masks, as the haze problem is probably staying for at least a month. Personally, I use Nasal Irrigation (Neilmed Sinus Rinse), which has tremendously helped my nose during this haze period. It can help clear out dust and mucus trapped in the nose.

[S$89.90][Clean Air]2015 Air Purifier Singapore brand and 1 year warranty with HEPA Activated Carbon UV-C germicidal killer lamp silent operation and high efficiency etc
WWW.QOO10.SG

[S$19.90]Haze Prevention~ Nasal Rinse™- Flush out mucous~germs~bacteria~and dirt internally. Clear blocked nose and very soothing.
WWW.QOO10.SG
Previously, we proved that any subgroup of index 2 is normal. It turns out that there is a generalisation of this theorem. Let 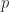 be the smallest prime divisor of a group
be the smallest prime divisor of a group  . Then, any subgroup
. Then, any subgroup  of index
of index 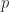 is normal in
is normal in  .
.
Proof: Let 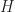 be a subgroup of
be a subgroup of  of index
of index 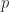 . Let
. Let  act on the left cosets of
act on the left cosets of 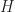 by left multiplication:
by left multiplication:  ,
, 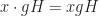 .
.
This group action induces a group homomorphism  .
.
Let  . If
. If  , then
, then  for all
for all  . In particular when g=1, xH=H, i.e.
. In particular when g=1, xH=H, i.e.  .
.
Thus  . In particular,
. In particular,  , since
, since  is a normal subgroup of
is a normal subgroup of  .
.
We have 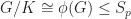 . Thus
. Thus  .
.
Also note that  . Note that
. Note that  since
since ![|G/K|=[G:H][H:K]=p[H:K]\geq p](https://s0.wp.com/latex.php?latex=%7CG%2FK%7C%3D%5BG%3AH%5D%5BH%3AK%5D%3Dp%5BH%3AK%5D%5Cgeq+p&bg=ffffff&fg=1a1a1a&s=0&c=20201002) .
.
Let  be a prime divisor of
be a prime divisor of  . Then
. Then 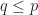 since
since  . Also,
. Also,  . Since
. Since 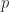 is the smallest prime divisor of
is the smallest prime divisor of  ,
,  . Therefore,
. Therefore, 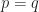 , i.e.
, i.e.  .
.
Then ![p=p[H:K] \implies [H:K]=1](https://s0.wp.com/latex.php?latex=p%3Dp%5BH%3AK%5D+%5Cimplies+%5BH%3AK%5D%3D1&bg=ffffff&fg=1a1a1a&s=0&c=20201002) , i.e. H=K. Thus, H is normal in G.
, i.e. H=K. Thus, H is normal in G.




