Author: tomcircle

Do not remember these:
$latex boxed {
cos 3A = 4cos^{3} A – 3cos A
}$

$latex boxed {displaystyle
int frac {dx}{sec x}
=
int
frac {1}{sec x}
frac {sec x + tan x}{sec x + tan x}dx
}&fg=aa0000
$

However, it helps, though, to remember:
“Nine Zulu Queens Rule China”
$latex boxed {
mathbb{N}subset mathbb{ Z }subset mathbb{ Q }subset mathbb{ R} subset mathbb{ C }
}&fg=00bb00&s=3
$

How Much Mathematics Should a Student Memorize?

Think of the 4th solution, if any, for this
“Monkey & Coconuts” Problem.

It was created by Nobel Physicist Prof Paul Dirac,  which he told another Chinese Nobel Physicist Prof Li ZhengDao (李政道)。
Pro Li wanted to test the Chinese young students in the first China Gifted Children University of 13 year-old kids, none of them could solve this problem (proved they are not so gifted after all for unknown problems :)

The first 2 solutions were solved by Prof Paul Richard Halmos,  the 3rd solved by myself using the Singapore Modelling Math (a modified version of Arithmetics from traditional Math taught in 1970s Chinese Secondary 1 “中学数学” in Singapore).

1st Solution: Higher Math: Sequence

https://tomcircle.wordpress.com/2013/03/30/monkeys-coconuts-problem/

2nd Solution: Linear Algebra: Eigenvalue and Eigenvector
https://tomcircle.wordpress.com/2013/03/30/solution-2-monkeys-coconuts/

3rd Solution: Singapore Modelling Math for PSLE (Primary 6)

https://tomcircle.wordpress.com/2013/03/30/solution-3-best-monkeys-coconuts/

4th Solution:
Any ?

UReddit Courses:

Modern Algebra (Abstract Algebra) Made Easy –

Part 0: Binary Operations

Part 1: Group

Part 2: Subgroup

Part 3: Cyclic Group & its Generator

Part 4: Permutations

Part 5: Orbits & Cycles

Part 6 : Cosets & Lagrange’s Theorem

Part 7 : Direct Products / Finite generated Abelian groups

Part 8: Group Homomorphism

Part 9: Quotient Groups

Part 10: Rings & Fields

Part 11: Integral Domain

Monster Group (code name “Moonshine”) is the largest group, discovered by two Cambridge Mathematicians John Conway and Simon Norton.

Monster Group – (1)

Monster Group (2):

John Conway: Life, Death and the Monster (3)

Ref:
1. Simon Norton (1952 -) – an eccentric mathematician who collects all British Railway Train Time Tables.
http://catalogue.nlb.gov.sg/cgi-bin/spydus.exe/ENQ/EXPNOS/BIBENQ?ENTRY=The%20genius%20in%20my%20basement&ENTRY_NAME=BS&ENTRY_TYPE=K&SORTS=DTE.DATE1.DESC%5DHBT.SOVR

2.
Finding Moonshine: A Mathematician’s Journey Through Symmetry by Marcus Du Sautoy

http://catalogue.nlb.gov.sg/cgi-bin/spydus.exe/FULL/EXPNOS/BIBENQ/6345422/5640834,2

Proof:

in Math logic,

$latex God subset Jesus text{ and}$
$latex Jesus subset God$
$latex implies $
$latex boxed {Jesus = God} $
[QED]

Tsung-tung Chang[張聰東] 1988:
“Indo-European vocabulary in Old Chinese: A new thesis on the emergence of Chinese language and civilization in the Late Neolithic Age”, Sino-Platonic Papers 7, Philadelphia.

This Chinese scholar wrote the 1988 paper on the Chinese language origin with the proto-Indo-European (proto IE).

Interestingly very similar ‘coincidence’ occurs in 1500 words between Chinese and proto IE:

Take -> 得 tek (ancient Chinese sound as in Fujian dialect today)
Mort -> 殁 mo
See -> 视 see
Cow -> 牛 gu
…

Click to access spp007_old_chinese.pdf

After the Tower of Babel, God confused the human into different languages, but by the linguistic ‘archaeology’ ‘Half Life’ Theory, we can deduce ~ 4,900 years ago the Chinese and the Germanic (English, Denmark, German …) shared the same common linguistic root.

The ancient Chinese scholar Xu Shen许慎(东汉 : 58 CE…

Einstein showed by Mathematics (the Riemann Geometry) to explain Space-Time curvature and the Gravity. It was later proved by the astrological discovery in Solar Eclipse.

Here, this professor made an experiment to demonstrate Einstein’s theory.

Gravity Visualized:

How did the NSA hack our emails?
Using Math in Elliptic curve…

NSA Surveillance (an extra bit) – Numberphile:

$latex zeta (-1) = 1 + 2 + 3 + 4 + … = – frac {1}{12} $

Why -1/12 is a gold nugget:

Natural Numbers (N) = {1,2,3, 4…}
1-dimension: a Line
2-dimension: a plane
n-dimensional flat space: a Vector Space

Now imagine in a world where we replace every natural number by vector space:
1 by a Line
2 by a Plane
n by a flat space Vector Space

Sum of numbers = Direct sum of vector space.
E.g. Add a 1-D Line to a 2-D Plane = 3-D Space

Product of numbers = Tensor Product (of two vector spaces of respective dimension m & n) with dimension m.n

This new world would be much interesting and richer than the Natural Number world: vector spaces have symmetries, whereas numbers are just numbers with no symmetries.
(Interesting): we can add 1 to 2 in only ONE way (1+2), but there are many ways to embed (add) a Line in a Plane (perpendicular, slanting in any angle, etc).
(Richer): the Lie Group SO(3)…

The young Russian doctor Sergei Arutyunyan was working with patients whose immune systems were rejecting transplanted kidneys.

The doctor has to decide whether to keep or remove it. If they kept the kidney, the patient could die, but if they remove it, the patient would need another long wait (or never) for another kidney.

The mathematician Edward Frankel helped him to analyze the collected data with ‘expert rules’ in a decision tree. (Note: this is like the Artificial Intelligence Rule-based Expert System, except no fuzzy math).

Love and Math by Edward Frenkel http://www.amazon.co.uk/dp/0465050743/ref=cm_sw_r_udp_awd_53swtb16779PY

“…There’s a long history of high caliber mathematicians finding their experiences with school mathematics alienating or irrelevant. “
Read here:
http://lesswrong.com/r/discussion/lw/2uz/fields_medalists_on_school_mathematics/

In Récoltes et Semailles Fields Medalist Alexander Grothendieck describes an experience of the type that Alain Connes mentions:

I can still recall the first “mathematics essay” (math test, or Composition Mathématique) , and that the teacher gave it a bad mark. It was to be a proof of “three cases in which triangles were congruent.” My proof wasn’t the official one in the textbook he followed religiously. All the same, I already knew that my proof was neither more nor less convincing than the one in the book, and that it was in accord with the traditional spirit of “gliding this figure over that one.” It was self-evident that this man was unable or unwilling to think for himself in judging the worth of a train of…

This professor criticized the lack of rigor in today’s math education, in particular, there exists universally a prevalent ‘ambiguous’ gap between high school and undergraduate math education.

I admire his great insight which is obvious to those postwar baby boomer generation.

I remember I was the last Singapore batch or so (early 70s) taking the full Euclidean Geometry course at 15 years old, and strangely in that year of Secondary 3 Math (equivalent to 3ème in Baccalaureate) my (Chinese) school had 2 separate math teacher for Geometry and Elementary/Additional (E./A.) Math.

Guess what ? the Geometry teacher was an Art teacher. It turned out it was a blessing in disguise, as my class of average Math students who hated E./A. Maths all scored 90% distinctions in Geometry. We did not treat Geometry like the other boring maths. The lady Art teacher started on the first day from Euclid’s 5 axioms…

One fine day when we reach above 80 years old, if the doctor accuses us of having dementia, then prove the doctor wrong by shocking him with 100-digit Pi memory 🙂

With Chinese single-syllable sound for numbers, better still if can sing it as a song, memorizing 100-digit pi is easy!

Best way to study abstract math is to use concrete examples, visualizable 2- or 3- dimensional mathematical ‘objects’.

Groups:
(Do not need to search too far…) Best example is the Integer Group (Z) with + operation, denoted as {Z, +}. (Note: Easy to verify it satisfies the group 4 properties: CAN I“.

It has infinite elements (infinite group)

It is a Discrete Group, because it jumps from one integer to another (1,2,3…, in digital sense).

The group of rotation of a round table, which consists of all points on a circle, is an infinite group. We can change the angle of rotation continously between 0 and 360 degrees, rotating around a geometrical shape – a circle. Such shapes are called Manifolds (流形).

All points of a manifold forms a Lie group.

Example: The group of rotations of a sphere around a central…

Durian & Group

Prove:  Any line L will cut a circle at most 2 points:

Factorize C(x,y) : (x+iy) (x-iy) = 1 in the complex plane.
So C  = {L1} U {L2}
where L1 and L2 are two lines

Examples:

Dim (Circle) in 2-dim plane = 1

As we approach near the neighborhood of the tangential point on the circle, the curvature of the circle disappears, there is no difference between the circle and the tangent line (dim = 1).

Hence, Dim (Circle) = 1

A point on a circle is determined by one independent variable only, which is the polar angle.

Note:
The dimension of the ambient space (2-dim plane) is not relevant to the dimension of the circle itself.

Dim (Sphere) in 3-dim Space = 2

The 2 variables (longitude, latitude) determine a position on the globe. Therefore dimension of a sphere is 2.

Interesting note:
Four Dimension Space (x, y, z, t): what we get if the 4th dimension time is fixed (frozen in time) ? We get a…

Shimura and Tanyama are two Japanese mathematicians first put up the conjecture in 1955, later the French mathematician André Weil re-discovered it in 1967.

The British Andrew Wiles proved the conjecture and used this theorem to prove the 380-year-old Fermat’s Last Theorem (FLT) in 1994.

It is concerning the study of these strange curves called Elliptic Curve with 2 variables cubic equation:

Example:
$latex boxed {y^{2} + y = x^{3} – x^{2}
} &fg=aa0000&s=3 $ — (I)

There are many solutions in integers N, real R or complex C numbers, but solutions in modulo N hide the most beautiful gem in Mathematics.

For modulo 5, the above equation has 4 solutions:
(x, y) = (0, 0)
(x, y) = (0, 4)
(x, y) = (1, 0)
(x, y) = (1, 4)

Note: the last solution when y=4,
Left side = 16 + 4 = 20 = 4×5 = 0…

“Math is nothing but a history of Group”

The Math teaching from primary schools to secondary / high schools should begin from the journey of Symmetry.

After all, the Universe is about Symmetry, from flowers to butterflies to our body, and the celestial body of planets. Mathematics is the language of the Universe, hence
Math = Symmetry

It was discovered by the 19th century French tragic genius Evariste Galois who, until the eve of his fatal death at 21, wrote about his Mathematical study of ambiguities.

Another French genius of the 20th century, Henri Poincaré, re-discovered this ambiguity which is Symmetry : Group, Differential Equation, etc.

Only in university we study the Group Theory to explore the Symmetry.

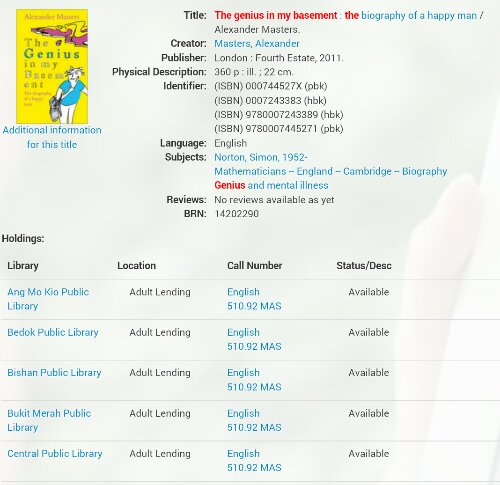
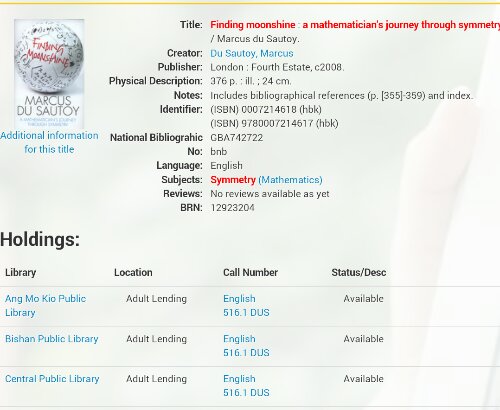
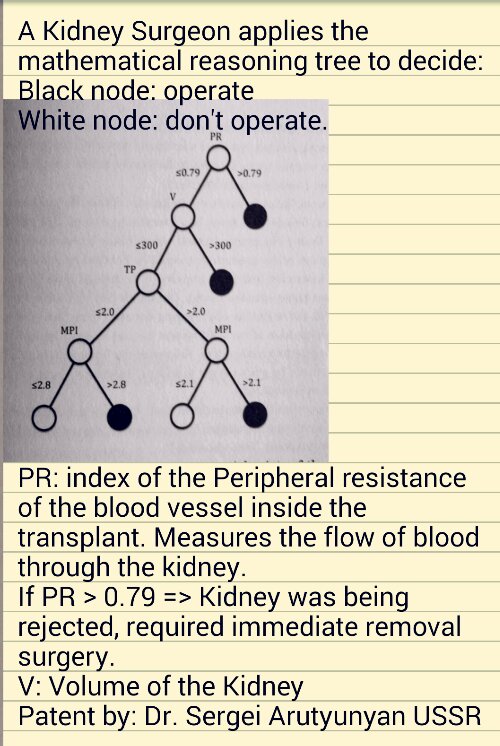
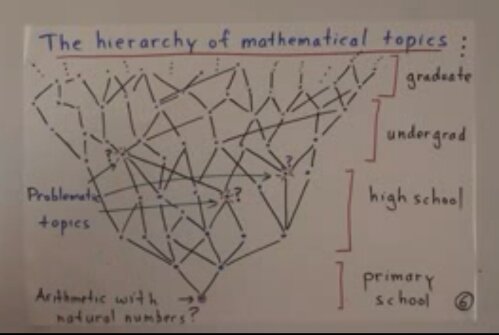
This addictive game “2048” is better than any other violent game like “The World of Warcraft”. At least it improves your math!

The video explains its principle and why you will never exceed 131,072.

It is binary arithmetic, or power of 2 = $latex 2^{n} &s=3$

Notice the rule of 0 & 1:
$latex 32 = 1underbrace {00000}_{5 : zero}$

Minus 2:
$latex 30 = 1111underbrace {0}_{1 : zero}$

Minus 4:
$latex 28 = 111underbrace {00}_{2 : zero}$

The maximum scenario whereby all 15 boxes are filled with the power of 2:

Final score (Maximum)
$latex 131,072 = 1underbrace {00,000,000,000,000,000}_{17: zero} = 2^{17} $

Case 1: The 16th box: – 2
$latex 131,070= underbrace {1111111111111111}_{16 : one} underbrace {0}_{1: zero}$

Case 2 (Maximum) : The 16th box: – 4
$latex 131,068 = underbrace {111,111,111,111,111}_{15 : one} underbrace {00}_{2: zero}$

Israel Gelfand, the student of Kolmogorov (the Russian equivalent of
Gauss), created in 1964 the famous VZMSh, a national Math Correspondence School.

He wrote: “4 important traits which are common to Math, Music, and
other arts and sciences:
1st Beauty
2nd Simplicity
3rd Precision
4th Crazy ideas.
”
The Russian mathematicians also built special Math-Physics schools:
Moscow School #7, #2, #57 (one of the best high school in the world, http://www.sch57.msk.ru) Leningrad Schools #30, #38, #239 (Perelman studied here)

Rukshin at 15 was a troubled russian kid with drink and violence, then a miracle happened: He fell in love with Math and turned all his creative, aggressive, and competitive energies toward it.

He tried to compete in Math olympiads, but outmatched by peers. Still he believed he knew how to win; he just could not do it himself.

He formed a team of schoolchildren a year younger than he and trained them.
At 19 he became an IMO coach who produced Perelman (Gold IMO & Fields/Clay Poincare Conjecture). In the decades since, his students took 70 IMO, include > 40 Golds.

Rukshin’s thoughts on IMO:

1. IMO is more like a sport. It has its coaches, clubs, practice sessions, competitions.

2. Natural ability is necessary but NOT sufficientfor success: The talented kid needs to have the right coach, the right team, the right kind of family…

The great Mathematician Israel Gelfand used to say:

“People think they don’t understand math, but it’s all about how you explain it to them.

If you ask a drunkard what number is larger , 2/3 or 3/5, he won’t be able to tell you. But if you rephrase the question:
What is better, 2 bottles of vodka for 3 people or 3 bottles of vodka for 5 people, he will tell you right away: 2 bottles for 3 people, of course.”

– Extract: “Love and Math”
by Edward Frenkel

http://books.google.com.sg/books?id=dc7yZKRizNQC&pg=RA1-PA129&lpg=RA1-PA129&dq=timothy+gowers+continuous+path+from+high+school+calculus&source=bl&ots=suLvmFtsJT&sig=yF7s9f5UozP25OO9zgDE_nPtRgI&hl=en&sa=X&ei=BZ1KU7y4EJSfiQf0v4DYCg&ved=0CA0Q6AEwAQ

Extract:

Timothy Gowers (Professor of Math, Cambridge, Fields Medalist)

The Basel Problem is:
$latex displaystyle sum_{k=1}^{infty} frac {1}{k^2} = frac {{pi}^2}{6}$

Euler was 28 years old when he proved that it converged.

The Basel Problem is also called the Riemann Zeta function: ζ(2).

He studied the function sin x which has zeroes,
i.e. sin x= 0 for
$latex x=npi, n = 0,pm1,pm 2, pm 3…$

In other words, we can factor sin x this way:
$latex sin x = x.(1+frac {x}{pi}) .(1-frac {x}{pi}).(1+frac {x}{2pi}). (1-frac {x}{2pi}).(1+frac {x}{3pi}). (1-frac {x}{3pi})…
&s=3$

Note: the right side any factor = 0 when
$latex x=npi, n = 0,pm1,pm 2, pm 3…$

$latex frac {sin x}{x}
= (1-frac {x^2}{1^{2}{{pi}^2}}).
(1-frac {x^2}{2^{2}{{pi}^2}}).
(1-frac {x^2}{3^{2}{{pi}^2}})…
&s=3
$

Note: $latex (1+a).(1-a)= 1 – a^{2}$

From Taylors series,
$latex
sin x = +frac {x}{1!} – frac {x^3}{3!} + frac {x^5}{5!} – frac {x^7}{7!} +…
&s=2$

$latex
frac {sin x}{x} = 1 – frac {x^2}{3!} + frac {x^4}{5!} –…

The Powerful Brains:

1. Spot the odd magic cube
2. “Drain man” Arithmetics
3. The mental Hanzi (汉字笔画) strokes
4. The ‘Breathing and Smelling’ (气息触觉) cognitive power of a blind.

I found (3) fantastic but the judge Dr. Wei disqualified her for being an “Asperger’s Syndrome” rather than a skill.

Which answer is the correct box ?

Ah Beng was asked to make a sentence using 1, 2, 3, 4, 5, 6, 7, 8, 9,10.

Not only did he do it 1 to 10, he did it again from 10 back to 1. This is what he came up with…..

1 day I go 2 climb a 3 outside a house to peep.  But the couple saw me, so I panic and 4 down. The man rushed out and wanted to 5 with me. I ran until I fell 6 and threw up. So I go into 7-eleven and grabbed some 8 to throw at him. Then I took a 9 and try to stab at him. 10 God he run away.

10 I put the 9 back and pay for the 8 and left 7-eleven.  Next day I called my boss and told him I was 6.  He said 5 , tomorrow also no need to…

Prime Secret: ζ(s).

There is a common proverb in my Chinese dialect Fujian spoken today in China Fujian province, Taiwan, Singapore and Malaysia, which says
“A nephew is like his maternal uncle”  外甥像母舅
In modern Biology we know mother passes some genes to her children. Some disease like colorblind is carried by mother down to her sons, the mother herself is immune but her brothers are colorblind as the nephews.
Interesting behavior, intelligence are also similarly inherited from mother and maternal uncles.

Two greatest mathematicians in the history, Newton and Gauss, were the lucky nephews from their maternal uncles who were highly educated to spot the nephew’s genius, although the boys’ parents were uneducated.

Newton’s father died early, mother Hannah Ayscough had a brother William Ayscough educated in Cambridge. William convinced Hannah to send the talented boy Newton to Cambridge.

Gauss’s father was a bricklayer, mother Dorothy Benz had a younger brother Friedrich…

Newton on how he made his discoveries:
“I keep the subject constantly before me and wait until the first dawnings open little by little into the full light.”

Newton was Lucasian prof of math at Cambridge. It was not obvious to
his students that he would become the greatest scientist in history.

His students wrote:
“… So few went to hear him, and fewer yet understood him, that
oftimes he did in a manner, for want of Hearers, read to ye Walls. ”

“He always kept close to his studies, very rarely went a visiting, &
had as few visitors… I never knew him take any Recreation or
Pastime, either in Riding out to take ye Air, Walking, Bowling, or any
other Exercise whatever, thinking all Hours lost, that was not spent
in his studies… He very rarely went to Dine in ye Hall…& then, if
He has not been minded, would…

First discovered by the Chinese Mathematician Minggatu 明安图 (清 康熙, 1730), later by the French (né Belgian) Ecole Polytechnique mathematicianEugène Charles Catalan (1814 – 1894).

Ref:

1. History:

2. Proof of Minggatu Catalan numbers

3. Monoid

4. Kleene Star

Extract from Catalan’s Retirement Speech:

Definition of Combination:
$latex displaystyle boxed {
{_n}C_k = frac {n!}{k!(n-k)!}
= binom{n}{k}
}$

Example:
$latex displaystyle
{_5}C_3 = frac {5!}{3!(5-3)!}
= frac {5!}{3!2!}
= frac {5.4.3.2.1}{3.2.1.2.1}
= frac {5.4.3}{3.2.1}
= binom{5}{3}
$

Combinations are even simpler to write with ‘Falling Factorial’ $latex x^{underline {n}}$

$latex x^{underline {n}} = underbrace {(x-0)(x-1)(x-2)… (x-(n-1))}_{n factors}$

$latex n! = n^{underline {n}} $

$latex displaystyle
binom{n}{k}
= frac {n!}{k!(n-k)!}
= frac {(n-0).(n-1)… (n-(k-1))}
{ (k-0).(k-1)… (k-(k-1)) }
= frac { n^{underline {k}}}
{k^{underline {k}}}
$

$latex displaystyle boxed {
binom{n}{k}
= frac { n^{underline {k}}}
{k^{underline {k}}}
}$

QED = Quod Erat Demonstrandum
or
Quite Easily Done

The order is important!

(a) & (b) have different meanings:

(a): For all M in R, there exists n in Nsuch that …

(b): There exists n in Nsuch that for all M in R, …

See also example below:
http://tomcircle.wordpress.com/2013/05/30/sequence-limit/

Ref: “The Math Girls”

$latex (2^0 +2^1 + 2^2 +…). (3^0 +3^1 + 3^2 +…)
$
$latex = (2^{0}3^{0})+ (2^{0}3^{1}+ 2^{1} 3^{0}) + (2^{0} 3^{2} + 2^{1} 3^{1} + 2^{2} 3^{0} ) + …
$
$latex displaystyle
= sum_{n=0}^{infty}
sum_{k=0}^{n}
2^{k} 3^{n-k}
$

Let the sequence $latex left { a_{n} right }$ convolved with another sequence $latex left { b_{n} right }$

$latex boxed {
left { a_{n} right } = left { a_{0}, a_{1}, a_{2}, …, a_{n}, … right }
}$
Its correspondence $latex leftrightarrow $ the generating function:
$latex displaystyle boxed {
a(x) = sum_{k=0}^{n}a_{k}x^{k}
}$

$latex boxed {
left { b_{n} right } = left { b_{0}, b_{1}, b_{2}, …, b_{n}, … right }
}$
Its correspondence $latex leftrightarrow $ the generating function:
$latex displaystyle boxed {
b(x) = sum_{k=0}^{n}b_{k}x^{k}
}$

The convolution is $latex displaystyle boxed { left { a_{n}* b_{n} right } =
left { sum_{k=0}^{n} a_{k}b_{n-k}right }
&fg=aa0000&s=1}$

“…to discover the equation in the first place, using the important method of generating functions, which is a valuable technique for solving so many problems.” – “The Art of Computer Programming Volume I”

Example:
Fibonacci sequence: {0, 1, 1, 2, 3, 5, 8, 13…}

Definition of the Fibonacci sequence as a recurrence relation:
$latex
boxed{
F_{n}=
begin{cases}
0, & text{for }n=0
1, & text{for }n=1
F_{n-2} + F_{n-1} , & text{for } n geq { 2}
end{cases}
}
$

This definition is not so useful in computation, we want to find a general term formula $latex F_{n}$ in terms of n.

Step 1: Find the generating function F(x)

The correspondence below:
Sequence $latex leftrightarrow $ Generating…

Chapter 3 on Rotation is excellent ! He combines Analytic Geometry, Linear Algebra (Matrix) , and Physics (Rotation) into “one same thing” to show the beauty of Mathematics:

The following matrix represents a rotation $latex rho (theta)$ by an angle $latex theta$:

$latex begin{pmatrix}
cos {theta} & -sin {theta}
sin {theta} & cos {theta}
end{pmatrix}
$

Rotate by $latex 2theta $ will be:
$latex begin{pmatrix}
cos {2theta} & -sin {2theta}
sin {2theta} & cos {2theta}
end{pmatrix}
$

Which is equivalent to rotate 2 successive angle of $latex theta $:
$latex rho (theta) .rho (theta) = rho^2 (theta) $:

$latex begin{pmatrix}
cos {theta} & -sin {theta}
sin {theta} & cos {theta}
end{pmatrix}^2
$
= $latex begin{pmatrix}
cos {theta} & -sin {theta}
sin {theta} & cos {theta}
end{pmatrix} $ $latex begin{pmatrix}
cos {theta} & -sin {theta}
sin {theta} & cos {theta}
end{pmatrix}$
= $latex begin{pmatrix}
cos ^2 {theta} – sin ^2 {theta…

Answer = 40

My nephew gets confused drawing exponential curves with many variations:
$latex e^{ax} $

If $latex -e^{ax} $, then reverse the y values, that is flip the curve over x-axis.

The 3 ancient Greek Problems are:
1. Trisect a Triangle
2. Square a circle
3. Doubling a Cube

Why restrict using only unmarked ruler ?
Answer: Using a Straight line: $latex boxed{ y = mx + c } $

Why a compass?
Answer: Using a Circle: $latex boxed{ x^2 + y^2 = r^2 }$

The 3 Greek Problems have been proven by 19th Century impossible to solve with only a straight line and a circle.

Calculate:
$Latex displaystyle
2^{2^{2^{2^{2^{ -infty} }}}}
$

Answer : 16

[Source: ]
D. Knuth “Digital Typography”

If we were to choose only 3 greatest scientists in the entire human history, who excelled in every field of science and mathematics, they are:
1) Archimedes
2) Issac Newton
3) Carl Friedrich Gauss

Let’s see how Gauss became a great scientist in his formative years in the university, it would give us a clue by knowing what kind of books did he read ?

Carl Friedrich Gauss was awarded a 3-year ‘overseas’ scholarship to study in Göttingen University (located in the neighboring state Hanover) by his own state sponsor the Duke of Brunswick.

Gauss chose Göttingen University because of its rich collection of books.
During the 3 years, he read very widely on average 8 books in a month.

Below was his student days’ library records:

1795-1796 (1st semister): total 35 books
Math (M) :1 ,
Astrology (A):2,
History/Philosophy (H): 1,
Literature/ Language (L): 15,
Science Journal (S): 16