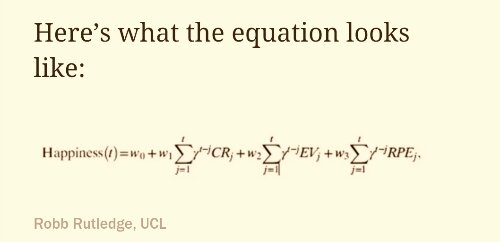UHG39: Rational trigonometry: an overview:
(Rational number only)
This is a revolutionary approach (2005) to teach Secondary / High school Trigonometry by using purely algebra, no geometry and no picture, no sine, cosine, tangent, etc.
New concepts:
Vector as an order pair (x, y)
Quadrance = magnitude of vector
Perpendicular of 2 vectors
Parallel
Spread (angle between 2 vectors)
Amazon Book by the Dr. NJ Wildburger:
https://memorado.com/iqtest?r=132#.U-Gemk463mf.facebook
You should get easily around 126 to 134 in IQ as my friends and I scored 🙂 Quite easy and encouraging !
http://www.businessinsider.sg/the-best-universities-in-every-country-2014-7/#.U9pB58kZ7qA
Australia: University of Sydney
Canada: University of Toronto
China: 北京大学
Japan: Tokyo University
Hong Kong: 香港大学
France: Ecole Normale Supérieure, Paris
India: Indian Institute of Technology, Delhi
Taiwan: 国立台湾大学
UK: Cambridge University
USA: Harvard University
MathHistory16: Differential Geometry
Two greatest grandmasters in Differential Geometry:
1. Gauss (Germany, 1777 -1855)
2. S. S. Chern 陈省声 (China, 1911 – 2004)
http://vimeo.com/m/16185312
《国宝档案》 20140407 紫禁城里的外国人—— 利玛窦 Matteo Ricci, Italian Jesuit: 中国”几何”之父。
《国宝档案》 20140408 紫禁城里的外国人——汤若望, German Jesuit
《国宝档案》 20140409 紫禁城里的外国人——南怀仁, Belgian Jesuit
《国宝档案》 20140411 紫禁城里的外国人——蒋友仁, French Jesuit
Discoverer of 易经 Yijing = Binary Mathematics 白晋 French Jesuit “The Louis 14 King’s Mathematician”
If you want your kids to grow up with Math talent, start young in Music, be it playing simple drum or flute, later at age 4 or 5 progressing to piano or violin, along the way pick up musical theory…
Notice that great mathematicians (or Physicists the close cousins of Math) are often music talents, but the converse not true! Einstein performed violin with an orchestra formed by a group of Nobel Prize Physicists; never heard Mozart or any great musicians proofed any Math Conjectures.
http://www.thecrimson.com/article/1988/11/30/music-math-a-common-equation/?page=3
Landau’s beautiful proofs:
1= cos 0 = cos (x-x)
Opening cos (x-x):
1 = cos x.cos (-x) – sin x.sin (-x)
=> 1= cos² x + sin² x
[QED]
Let cos x= b/c, sin x = a/c
1= (b/c)² + (a/c)²
c² = b² + a²
=> Pythagoras Theorem
[QED]
Landau (1877-1938) was the successor of Minkowski at the Gottingen University (Math) before WW II.
Prime Numbers
God multiplies Primes: Fundamental Law of Arithmetic (Euclid):
Any number (n) can be UNIQUELY Prime Factorized: n = P1 x P2 x …Pn
e.g. 12= 2 x 2 x 3,
28=2 x 2 x7
Men add Primes: Goldbach Conjecture.
2n = P1+P2
e.g. 12= 5 + 7, 28 = 17 + 11, 30 = 11+19
Chen Theorem 陈景润 @1966‘1+2’ 陈式定理
2n= p1 + p2 (Goldbach Conjecture “1+1“)
or
2n = p1+ p2*p3 (Chen Theorem “1+2″)
Examples:
62 = 43 + 19
62= 7 + 5*11
4 Levels:
L1. S&T (See & Touch) Concrete: 1 apple, 2 oranges…
e.g. Math Modeling: visualise the problem [Primary School]
L2. S~T (See, no Touch but can guess):
e.g. Guess x,y for 2x+3y=8 ? [Secondary School]
e.g. Chimpanzees can guess where you hide the banana.
L3. ~S~T&I (no See, no Touch but Imagine):
e.g. Complex i = [Junior College].
L4. ~S~T~I (no See, no Touch, no imagine)
e.g. Abstract Math: Galois Group, ε-δ Analysis, Ring, Field, etc. [University]
1. Galois’s mother home-schooling him Latin & other languages before entering Lycée Louis-Le-Grand.
2. William Hamilton: knew 15 languages include Chinese before discovered Quarternions (1,i,j,k) on Monday 16 Oct 1843 walking along Brougham Bridge, Ireland.
3. Pascal, Descartes are philosopher good in writing.
4. Gauss learnt even at old age Russian to read Lobatschefsky’s Non-Euclidean Geometry
5. Cauchy’s father heeded the advice of his neighbour Laplace to teach young Cauchy language before mathematics.
Good Mathematics [Lagrange’s definition]
1. Easy to understand by people on the streets
2. Difficult to solve
Example: Fermat’s Last Theorem
秦九韶 Qin Jiushao(1202-1261 AD): http://en.wikipedia.org/wiki/Qin_Jiushao
A Southern Song dynasty (南宋) officer. During his 3-yr leaves when his mother died, he generalised 孙子算经 (4th century)’s “Chinese Remainder Theorem” in ‘大衍求一术’. After leaves, he went back to chase money & women, produced no more Maths.
Note: ‘求一’: solve a.X ≡ 1 (mod b); a < b
Topology (by Poincaré)
Moniker “Rubber-Sheet Geometry“, compared with Geometry’s ‘rigid objects‘.
[Greek]= τοΠοζ(Place) λΟγια(Study)
[Latin]= Analysis Situs (Situation)
1. Remove (invariants) of geometry:
2. Preserve ‘Neighbourhood’ (Nearness)
3. Elastic deformation (stretch, bend, twist)
Paul Erdös liked to talk about ‘The Book’, in which God maintains the perfect proofs for mathematical theorems (& he ‘peeped’ 1,000 from there).
Primes (Landau’s trick)
List down systematically the primes below n < 4,000
Start with 2
2×2= 4 => take 3 (<4)
< 2×3 =6 => 5
< 2×5 =10 =>7
< 2×7 =14 => 13
…
23, 43, 83, 163, 317, 631, 1259, 2503, (4001)
Learn Math With Own Example Space
G. Polya / Paul Halmos advocate getting math students to construct not just one but classes of examples to:
1. Extend & enrich own Example Spaces;
2. Develop full appreciation of concepts, definitions, techniques that they are taught.
[Polya, Halmos, Feynman]: they collect and build a personal ‘repertoire’ of “Examples Space” (include counter-examples) for each abstract math idea, which they can relate to a concrete object.
Examples:
Group abelian = (Z,+)
Ring = Z
Principal Ideal = nZ
Equivalence Relation = mod (n)
Cosets = {3Z, 1+3Z, 2+3Z}
…
Given: a unit length.
Use only a straightedge (ruler without markings) & a compass.
Prove: we can construct a line segment of √n for all n ∈N.
Proof:
1) n=1 (given).
2) Assume true for n, i.e. can construct √n
3) Construct a right-angled triangle with height = 1, base= √n
=> hypotenuse = $latex sqrt {n+1} $
=> True for n+1
Therefore true for all n ∈N [QED]
Prof ST Yau (Fields Medal, Harvard Math Dean)
OUHK – 數學在今日社會的應用–丘成桐教授 (第一部分):
1. Wavelet Data Compression Algorithm:
2. RSA Encryption
OUHK – 數學在今日社會的應用–丘成桐教授 (第二部分):
OUHK – 數學在今日社會的應用–丘成桐教授 (第三部分):
3. Akamai Network Distribution
OUHK – 數學在今日社會的應用–丘成桐教授 (第四部分):
4. Insurance Risks (Actuary)
OUHK – 數學在今日社會的應用–丘成桐教授 (第五部分):
5. GOOGLE Search:
OUHK – 數學在今日社會的應用–丘成桐教授 (第六部分):
6 不急功近利走捷径
7. 做大数学家成功之道:
– 对数学浓厚的兴趣
– 行则的培养: 不肤浅, 不偷功，不炫耀。
– 打好基本功
See also:
These are the top 10 tough Mathematics:
1. Motivic cohomology or cohomology Theory 上同调理论
2. Langlands Functoriality Conjecture
3. Advanced Number Theory (eg. Fermat’s Last Theorem) 高等数论
4. Quantum Group 量子群
5. Infinite Dimensional Banach Space 无穷维度巴拿哈空间
6. Local and Micro-local Analysis of Large Finite Group 大有限群之局部与微局分析
7. Large and Inaccessible Cardinals 大与不可达基数
8. Algebraic Topology 代数拓扑学
9. Super-String Theory 超弦论
10. Langlands Theory 非阿贝尔互反性，自守性表现和模数变化
Algebraic Topology: using algebra (eg. Group Theory) to study geometrical shapes.
Difference between Algebraic Topology and Algebraic Geometry (see the previous blog):
“Algebra is the written Geometry,
Geometry is the drawn Algebra.”
— Sophie Germain (France, 19 CE)
Algebraic Geometry is the study of the zeroes (or roots) of Polynomials.
Birkhoff 是哈佛土生土長培养的学生, 数学大师, 他又培养了50个博士, 教育了7,500学生成为世界一流数学家。
Do we really live in 10-dimensional Space ? Harvard Prof S.T. Yau (1st Chinese Fields Medalist) talked on the inner space of Geometry and String Theory in Physics:
我們真的活在十維時空裡嗎?丘成桐院士從幾何和弦論談空間的內在形狀:
See also :
https://tomcircle.wordpress.com/2013/04/01/st-yao%e4%b8%98%e6%88%90%e6%a1%90/
Test if you have Mathematical Mind ?
Do not scroll to below to see the answer until you have tried …
…
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Answer:
Since 1 = 11,
of course 11 = 1
That is the mathematical meaning of ‘=’
Hua Luogeng (华罗庚) urged using the daily 10-20 mins intervals while waiting for buses, queues, idle times, make it at least 1 hour a day to read Math books which you carry along with you.
Hua advised on speedy self-learning Math :
1) Choose the Best book on the Topic written by the Master (say, Abstract Algebra), read completely and do the exercises.
2) Read other reference books. Read only those new topics not covered in 1).
If not much new things, return them to bookshelf. This way speed up reading many books in short time.
3) Then read International renown Math Journals.
Beware 90% are copy-cats or rubbish by University lecturers to meet their yearly publishing quota. Only < 10% are masterpieces.
4) Pick one topic to do your independent research.
5) Discuss with friends with better knowledge in the field.
This way you can be a Master in…
View original post 7 more words
华罗庚 《数论导引 》序言
Preface on “Introduction to Number Theory” by Hua Luogeng (1950).
“Math evolved from concrete to abstract, the former is the source of inspiration of the latter. One cannot just study the abstract definitions and theorems without going back to the source of concrete examples, which prove valuable applications in Physics and other sciences.”
“Mathematics, in essence, is about the study of Shapes and Numbers. From Shapes give rise to the Geometrical Intuition, from Numbers give the Relationship and Concepts ”
2003/7/13 台大访问笔记则要:
http://blog.sina.cn/dpool/blog/s/blog_c24597bf0101ctdp.html
突破瓶頸: “先上对车, 后补上票”
Holistic Approach to Attack Math :
新酒进旧瓶, 可以突破: 勤能补拙
10岁的启蒙书:
现代”科举”考场失意:
文学与数学相通:Intuition
Ref: 白居易写给元稹的《与元九书》
如何教好数学?
Shimura Modular Form:
好书推荐: 华罗庚的《数论导引》 , 华的剑桥老师Hardy…
解析数论 Analytic Number Theory:
选对导师和有兴趣的题目
On Riemann Hypothesis:
教授會武術，流氓也擋不住 – 川大教授課堂利用數學公式劈磚:
This science professor uses kungfu to demonstrate 2 simple Physics mathematical formulas :
2 formulas:
Impulse : http://www.physicsclassroom.com/class/momentum/u4l1b.cfm
Lever : http://www.theclevver.com/theory.htm
Tolstoy’s “War and Peace”:
“Only by taking an infinitesimal small unit for observation (the differential of history, that is, the individual tendencies of men) and attaining to the art of integrating them (that is, finding the sum of these infinitesimals) can we hope to arrive at the laws of history.”
National University of Singapore (21st),
Nanyang Technological University (91-100th)
http://www.timeshighereducation.co.uk/world-university-rankings/2014/reputation-ranking
Asia Ranking:
NUS (2nd) after The University of Tokyo (1st).
http://www.timeshighereducation.co.uk/world-university-rankings/2013-14/regional-ranking/region/asia
This is the first appearance of
$latex boxed {pi = 3 }$
in any human’s text in history.
45 feet / 15 feet = 3
The French Mathematician and Physicist Joseph Fourier proved
e is irrational,
Another French mathematician Charles Hermite went further: e belongs to another mathematical world:
e is transcendental.
Hermite’s German student Lindermann followed the same method, proved:
pi is also transcendental.
Introduction to Category Theory 1:
Course Overview:
Category Theory = Abstract Algebra of Functions
Lambda Calculus = Calculus of Functions
Lambda Calculus = Category
History:
$latex cap bigotimes$
Introduction to Category Theory (2) Monoids 么群
Introduction to Category Theory (3)Real lecture begins from here: Categories, Functors, Natural Transformation:
1. Category Definition:
1a) Examples of Categories:
Excellent example on “Natural Transformation“:
Ref: Classic Textbook
范畴论 Category Theory :
1. Matrix (M): stretch & twist space
2. Vector (v): a distance along some direction
3. M.v = v’ stretched & twisted by M
Some directions are special:-
a) v stretched but not twisted = Eigenvector;
b) The amount of stretch = constant = Eigenvalue (λ)
Let M the matrix, λ its eigenvalue,
v eigenvector.
By definition: M.v = λ.v
v = I.v (I identity matrix)
M.v = λI.v
(M – λI).v=0
As v is non-zero,
1. Determinant (M- λI) =0 => find λ
2. M.v = λ.v => find v
Note1: Why call Eigenvalue ?
From German: “Die dem Problem eigentuemlichen Werte”
= “The values belonging to this problem”
=> eigenWerte = EigenValue
Eigenvalue also called ‘characteristic values’ or ‘autovalues’.
Eigen in English = Characteristic (but already used for Field).
Note2: Schrödinger Quantum equation’s Eigenvalue = Maximum probability of electron presence at the orbit…
View original post 12 more words
Relationship-Mapping-Inverse (RMI)
(invented by Prof Xu Lizhi 徐利治 中国数学家 http://baike.baidu.com/view/6383.htm)
Find Z = a*b
By RMI Technique:
Let f Homomorphism: f(a*b) = f(a)+f(b)
Let f = log
log: R+ –> R
=> log (a*b) = log a + log b
1. Calculate log a (=X), log b (=Y)
2. X+Y = log (a*b)
3. Find Inverse log (a*b)
4. ANSWER: Z = a*b
Prove:
$latex sqrt{2}^{sqrt{2}^{sqrt{2}}}= 2$
1. Take f = log for Mapping:
$latex logsqrt{2}^{sqrt{2}^{sqrt{2}}} $
$latex = sqrt{2}logsqrt{2}^{sqrt{2}}$
$latex = sqrt{2}sqrt{2}logsqrt{2} $
$latex = 2logsqrt{2} $
$latex = log (sqrt{2})^2 $
$latex = log 2$
2. Inverse of log (bijective):
$latex log sqrt{2}^{sqrt{2}^{sqrt{2}}}= log 2$
$latex sqrt{2}^{sqrt{2}^{sqrt{2}}}= 2$
New Geometry (新几何) invented by Zhang JingZhong (張景中) derived from 2 basic theorems:
1) Triangles internal angles =180º
2) Triangle Area = ½ base * height
=> derive all geometry
=> trigonometry
=> algebra
(These 3 maths are linked, unlike current syllabus taught separately)
The powerful Area (Δ) Proof Techniques:
1) Common Height:
Line AMB, P outside line
Δ PAM / Δ PBM = AM/BM
2) Common 1 Side (PQ):
Lines AB and PQ meet at M
Δ APQ /Δ BPQ = AM/BM
3) Common 1 Angle:
∠ABC=∠XYZ (or ∠ABC+∠XYZ = ∏ )
Δ ABC /Δ XYZ= AB.BC /XY.YZ
These 3 theorems can prove Butterfly and tough IMO problems.
Butterfly Theorem
In a circle draw a chord PQ with mid-point M. Through M draw 2 chords AB, CD. Join AD, BC cut PQ at X, Y resp. (Butterfly M)
1. Prove: M = mid-point of XY
http://gogeometry.com/GeometryButterfly.html
2. If circle changed to ellipse, still true?
Yes. Affine transformation from circle elongated to ellipse, like distorted image through funny mirror => still MX = MY
Butterfly theorem (Pho
Mathtuition88 