Author: tomcircle

http://www.youtube.com/watch?v=lJhmJJ_q6Go&NR=1

The lyrics to the song can be found in “Contemporary Abstract Algebra” (Seventh Edition) by Joseph A. Gallian

(ISBN 978-0-547-16509-7) pages 422 & 423.

https://www.theverge.com/2017/9/2/16247282/euclids-elements-kroncker-wallis-math-text-beautiful-minimalist-kickstarter

Little print-edition of Math Classics: Euclidean 《The Elements》(几何原理) – the second printing by volume after 《The Bible》.

The Euclidean Geometry was less emphasised in Secondary school from 1970s in the world (80s in Singapore) to be replaced by Vector Geometry (UK/USA) and Abstract Linear Algebra aka Vector Space / Affine Geometry (in France). It was a pedagogical mistake now these countries recognise – never “Throw the baby (Euclidean Geometry) together with the bath water (Old Maths )”.

IMO Competition usually has 2 out of 6 problems in Euclidean Geometry but no modern math or Calculus, reason being to cater for 100+ countries still with Classical Math. That’s why the Asian countries – South Korea (2017 IMO Champion), China (2nd IMO 2017), Vietnam (3rd IMO 2017) , HK, Taiwan, Thailand, – with old syllabus are top IMO but not the Advanced countries (France, UK, other European, Japan, USA, Singapore…).

https://medium.com/@cscalfani/so-you-want-to-be-a-functional-programmer-part-1-1f15e387e536

数学中代数的有两个名词：环，半群，请问环为什么叫做环，它和汉字里的环（字典中的意思）有什么相同之处；同样，半群为什么叫做半群，这个”半“字是怎么解释呢？

[葛利流，数学科技]

(I) 环和域
环 (Ring) 是德文, 这名词是David Hilbert发明的。
“环”最好的例子: 整数(Integer) 记作 Z (德文Zahl) 是个环。 他研究 Clock Arithmetic 时钟 是个 Modular Arithmetic (Mod 12)运算, 比如 15 = 3 mod 12
…
钟表上的整数 Z 数字 排成 一个钟的环状, 故称 此数是 “Zahl Ring” 整数 “环”。

Hilbert 的得意女弟子 Emile Noether 把 环论 发扬光大, 创造 “Noether Ring”。

如果 把 “12” 变成 任一素数 p , “环”就升级成”域” (Field) – 除了有环的( + – *) 运算, 还可以 (÷)。

Hilbert 发现 “环”有个重要性质是含有 “理想” (Ideal) – 理想 * 任何”外面”的东西 还回来”里面”。
例子: Z Ring 里有 “0”, 2Z, nZ…
0 * 任何Z数 => 回来 “0家族里面”
偶数 2 * 任何Z数 => 回来” 偶数 (2Z)家族里面”
…
大名鼎鼎的中国古代算术”韩信点兵”就是 含有 “环 和理想”的理论。

(II) 群 Group / 半群 Semi-Group / 幺半群MonoId
Group 群 有4个性质 C.A.N.I.
C: Close 封闭性
A: Associative 连续性
N: Neutral (or Identity = Id) 幺元
I: Inverse 逆元

Semi-Group 半群 只有2个性质: C.A.

Monoid 么半群 : C.A. + N (= Id) => Mono + Id

https://www.zhihu.com/question/20564445/answer/233486338

Answer: 10 (Yes!) but why ?

…(see explanation here )

https://vulcanpost.com/613827/zapzap-math-malaysia-education-app/

Key Points:

• Pure Function
• Partial Function
• Total Function

View at Medium.com

Very good introduction of Modern Math concept “Group” to secondary school math students by an American high school teacher.

https://www.quantamagazine.org/symmetry-algebra-and-the-monster-20170817/

Summary:

• Symmetry of a Square
• Isometry (*) or Rigid Motion (刚体运动) = no change in shape and size after a transformation
• What is a Group (群 “CAN I” ) ? = Closure Associative Neutral Inverse
• Monster Group = God ?
• String Theory: Higgs boson (玻色子) aka “God Particles”

Note (*): “保距映射” (Isometry），是指在度量空间 (metric space) 之中保持距离不变的”同构“关系 (Isomorphism) 。几何学中的对应概念是 “全等变换”。

A new alternative to the UK Mathematica’s “Wolfram Alpha” online tool:

http://www.makeuseof.com/tag/not-wolfram-alpha-solve-math-equation-symbolab/

[Original Financial Times Article] Google: UK maths books fail DfE test

$latex boxed {text {The Ideal Math = (Chinese + English) * French }}&fg=aa0000&s=3 $

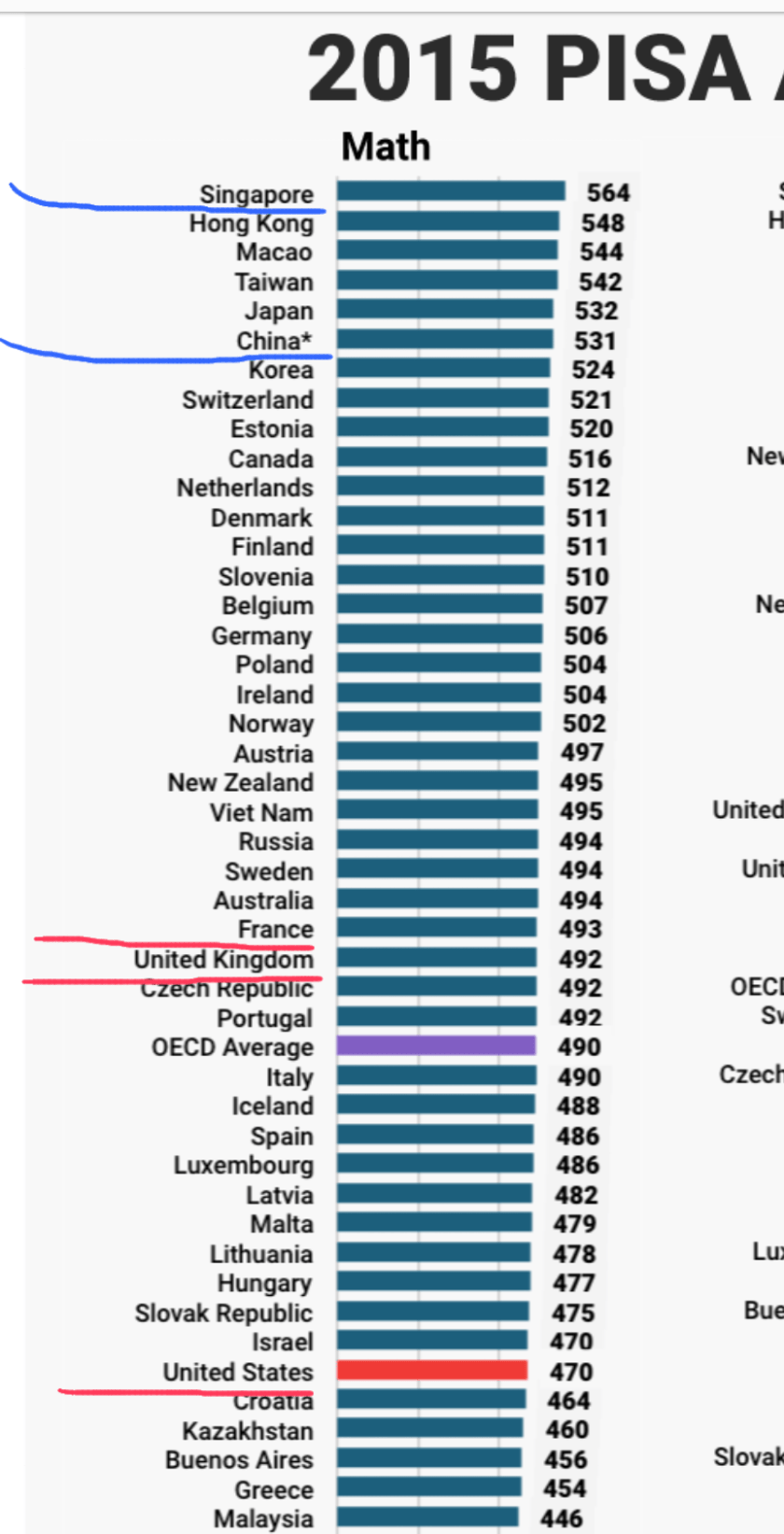
UK, USA, France are copying Chinese Math (from which the “Singapore Modeling Math” derived) in Primary schools, this proves my above-mentioned “Ideal Math” formula is correct. The 2 Asian countries were top in 2015 PISA Math Test for 15-year-old students, while UK was ranked 27th.

It remains to see if China / Singapore reciprocate the French Math theoretical foundation rigor in High Schools (Junior Colleges) and in the first 2 years of undergraduates for STEM (Science, Technology, Engineering, Math) students.

Compared with Fields Medals (equivalent to Nobel Prize in Math), the picture is reversed – where USA, France and UK are top. The secret lies in the formula : the multiplying factor – (* French), ie the math theoretical foundation notably…

Many excellent Math students after leaving universities more than 10 years forget 90% of math they learned, save some primary school arithmetics – few could do Singapore PSLE Modelling Math or solve quadratic equations.

The “Story-Telling” memory technique via “Signposts” can be used to reconstruct math from first principles:

https://medium.com/@fjmubeen/how-not-to-memorise-mathematics-98fef71aefcf

Note: Lewis Carroll: the author of “Alice in wonderland”

Cambridge Professor Tim Gowers (Fields Medalist) suggested the similar pedagogy of “Memorise by First Principles”.

https://futurism.com/math-help-treat-diseases-develop-better-vaccines/

Revision: Modulus Arithmetics

(1/2) Fermat Little Theorem

(1/2) Chinese Theorem

(Note: This is the “RING” foundation of “The Chinese Remainder Theorem” which deals with remainders )

$latex boxed { text {Ideal Math Education } = (C + E) * F}&fg=aa0000&s=3$

C = Chinese 中文 = Primary school Arithematics sans “Algebra” (= Singapore Modeling Math). Abacus-Algorithmic thinking.

E = English = Secondary School Math
=> Applied, Tricky, Math Olympiad-style
=> Engineering, Business, Applied Science.

F = Français (French) = High-school / Baccalaureate & University Math = Theoretical, Abstract
=> Rigorous Math Philosophy for Advanced Concepts
=> New frontier Scientific Research.

Why (C+E) ?
C + E = Basic Math Foundation.

Why * F ?
If multiply by Theoretical F, like flying with added wings (如虎添翅)。

However,
if (C+E) -> 0 (less applied), or
if F -> 0 (lack theories),
then Total Math Education -> 0.

One basket of eggs.
1粒1粒拿，正好拿完。
Remove 1 by 1, nothing left in basket.

2粒2粒拿，还剩1粒。
Remove 2 by 2, one left in basket.

3粒3粒拿，正好拿完。
Remove 3 by 3, nothing left in basket.

4粒4粒拿，还剩1粒。
Remove 4 by 4, one left in basket.

5粒5粒拿，还差1粒才能拿完。
Remove 5 by 5, short of one to complete.

6粒6粒拿，还剩3粒。
Remove 6 by 6, 3 left in basket.

7粒7粒拿，正好拿完。
Remove 7 by 7, nothing left in basket.

8粒8粒拿，还剩1粒。
Remove 8 by 8, one left in basket.

9粒9粒拿，正好拿完。
Remove 9 by 9, nothing left in basket.

请问筐里最少有几粒鸡蛋 ？
At least how many eggs are there in the basket?

[Hint] This is a Chinese Remainder Problem (” 韩信点兵“)

—— [Solution] —–

Let there be minimum X eggs in the basket.

Remove 1 by 1, nothing left in basket:
X = 0 mod (1) …[1]
=> trivial & useless !

Remove 2 by 2, one left in basket:
X =…

“Categories for Dummies”
(French)

Example 1:

Paris (P) -> Rome (R) -> Amsterdam (A)
Objects: cities {P, R , A}
Morphism (Arrow): railway

• Identity: railway within the city
• Associative: (P -> R) -> A = P -> (R ->A)

=> Category

Example 2:
A, B are categories
functor f : A -> B

f (B) has the “information” on A, with some loss of information since f may not be a MONOMORPHISM.

Example 3: Natural Transformation

A = 0 1 2 3 4
f : A -> B

B = Ladder steps:
f(0)|
f(1)|
f(2)|
f(3)|

g : A -> B

B = Staircase steps :
g(0)||
g(1)||
g(2)||
g(3)||

Natural Transformation: =>α

α : f (i) => g (i)

f(0)| =>g(0)||
f(1)|=>g(1)||
f(2)|=>g(2)||
f(3)|=>g(3)||

α transforms naturally the Ladder to the Staircase.

https://sites.google.com/site/logiquecategorique/dcm

4. Category, Logic and IT

Tom Leinster

N = 0 : 0-Cat

• => Set, 0-morphism = function

N= 1: 1-Cat

• => Cat, 1-morphism = functor

N= 2: 2-Cat

• => 2-morphism = Natural Transformation

$latex text {f, g : 1-morphism }$

$latex alpha :: beta text { Natural Transformations : 2-morphism }$

Definition of n-Category:

Composition:

0-Cat : Set
1-Cat : Cat

Examples of n-Categories:

• Manifold
• Top (Topological Space) : 2-morphism = homotopy

Ref:

Best Technical Category Theory Book (2016) by Tom Leinster (Cambridge Press): “Basic Category Theory”

(Free downloadfrom arxiv)

Dr. Eugenia Cheng – Professor of Category Theory (Chicago University)

Author of the Best Selling Category Book Book : (for readers from 7-year-old to high school and undergraduate students)

“How to Bake Pi ?- an Edible Exploration to the Mathematics of Mathematics”

[Loan from NLB(eg. AMK Branch)]

Illustrations:

• Factors of 30 = {2, 3, 5, 6, 10, 15, 30} which form a Cube with these factors as the vertices.
• Knots
• Bach music
• Associativity: (sugar + milk + egg )
• Button cake = order 2 group (0,1)
• Bed mattress = rotate, flip, flop
• Icosahedral virus

Ref:

Best Technical Category Theory Book (2016) by Tom Leinster (Cambridge Press): “Basic Category Theory”

(Free downloadfrom arxiv)

2017

Keywords:

• Category
• Monad = Monoid + Endofunctor

Category Theory is replacing Set Theory as the foundation of Math. Nowadays, few Advanced Math papers are written without using Category to explain, and this trend is spreading to IT through Functional Programming languages (Google’s Kotlin, Haskell, Clojure…) - the latest paradigm to replace Object-Oriented languages like Java, C++, etc, as a safer “Strong Typed” languages for AI, BIG DATA…

$latex boxed {text {Type = Category }}&fg=aa0000&s=3$

Examples of “Types” in IT:

• Integers
• Real
• Double
• Boolean
• String
• etc

Remember when you cancel a common factor at both sides of an equation, you must check if the factor is non-zero, otherwise you would miss some answers.

This is about Cancellation Law, related tofewNumber Theory Properties :

• Zero Divisors,
• Integral Domain.

Origin of “Integral” => Integers

Definition of Integral Domian:

Property:Cancellation Law

Reading:

THEOREMS:(PROOF Here)

1. Every Field is an Integral Domain.
2. Every finite Integral Domain is a Field.

A weak South Korean Math studentJune Huhbecomes a top Mathematician in the Princeton Institute for Advanced Study by proving the Read’s Conjecture and Rota Conjecture.

“A path less taken to the peak of the Math World” :

https://www.quantamagazine.org/a-path-less-taken-to-the-peak-of-the-math-world-20170627/

This important idea is called Isomorphism 同构…

“Algebraic Topology” can detect the Multi-dimensional neural network in our brain – by studying the Homology (同调) and co-Homology (上同调) with the help of Linear Algebra (multi-dim Matrix) & Computers.

Homology = compute the number of “holes” in multi-dim space.

Neurons formed in the brain can be modeled in Math (Topology) by Simplex 单纯 (plural : Simplices), billions of them interconnected into a complex -“Simplicial Complex” (单纯复体)。

https://singularityhub.com/2017/06/21/is-there-a-multidimensional-mathematical-world-hidden-in-the-brains-computation/?from=timeline#.WUvPNsvmjqD

What is Math ?
https://infinityplusonemath.wordpress.com/2017/06/17/what-is-math/

• Mathematics= “that which is learned“ –(Pythagoras)

Math is not about calculation, it is understanding the nature, the universe, the philosophy (logic, intelligence – both “human” and “artificial”)…

What is Axiom, Lemma, Proposition ? Why rigorous Calculus was needed hundred years afterNewton & Leibnizhad invented it – “Epsilon-Delta” Analysis.

Difference between Riemann Integral & Lebesgue Integral ?

Singapore scores the 2017 PISA Test World’s First in Math.

Below is the “Singapore Math” shown by an USA School adopting the pedagogy.

I had the opportunity to meet the inventor of the “Singapore Math” Prof Lee PengYee (李彝义) in a Math seminar at NUS few years ago, who said he took the inspiration of the ancient Chinese math 算术 (literary means “Counting Technique” sans Algebra), combined with the PolyaProblem Solving Methodology, with a visual tool called “The Model Diagram”.

Note that this pedagogy is based on concrete visualisation, while good for majority of young students to learn computation and problem solving, it doesn’t train the opposite skill in “abstractness” which is required in university Advanced Math, where the French, Russian and USA university students excel more than the Asian cohorts.

The Ideal Math Education for the next 22ndCentury:

Singapore Math (Computation for…

Three mysterious Math Objects:

• Pi,
• Complex Numbers,
• Prime Numbers

are hiding in circle.

After the defeat in 1st match, Ke Jie said “AlphaGo is approaching God!”.

This version of AlphaGo is 10x more powerful than last year’s version which has beateb the South-korean Go player Lee.

https://www.theguardian.com/technology/2017/may/23/alphago-google-ai-beats-ke-jie-china-go

Kotlin is the “New Java” officially supported by Google from May 2017! It is less verbose (罗唆) than Java which is clumsy with boilerplates (样板), interoperates with Java on JVM, with modern functional programming features, and most importantly,it is Multi-Platform : Java, Android, Javascript, and future versions run as native codes on iOS, MacOS and Linux (Microsoft – work in progress). This eliminates the current headache of having to re-write the same applications for different platforms in different languages.

Google makes Kotlin a first-class language for writing Android apps

https://blog.plan99.net/kotlin-fp-3bf63a17d64a

Kotlin Tutorials:

https://kotlinlang.org/docs/tutorials/

https://developer.android.com/kotlin/get-started.html

Hands-on:

https://try.kotlinlang.org/#/Kotlin%20Koans/Introduction/Hello,%20world!/Task.kt

Two ways to program in Kotlin:

1) Google way: Download Android Studio 3.0 (with Kotlin and Java 8 Support):

https://www.xda-developers.com/you-can-download-the-canary-1-build-of-android-studio-now-supports-kotlin/

2) (A better way): use Jetbrains “Intelli IDEA for kotlin” (bundled with Kotlin)

https://kotlinlang.org/docs/tutorials/getting-started.html

Books:

https://antonioleiva.com/kotlin-android-developers-book/

https://www.amazon.com/gp/aw/s/ref=is_s_ss_i_5_6?k=kotlin+for+android+developers&sprefix=kotlin

Emmanuel Macron is the youngest French President (39) since Napoleon Bonaparte (40).

A brilliant student since young, he impressed his secondary school Drama teacher 24 years older, finally married her.

Like any genius (Einstein, Galois, Edison, …) who doesn’t adapt well in the traditional education system, Macron entered the prestigious and highly competitiveClasse Préparatoire (Art Stream) Lycée Henri IVin Paris to prepare for the “Concours” (法国抄袭自中国的)”科举” Entrance Examsin France’s top Ecole Normale Supérieure (ENS). Like the 19CE Math geniusEvariste Galoiswho failed the Ecole Polytechnique Concours twice in 2 consecutive years, Macron also failed ENS “Concours” in 2 consecutive years.

He revealed recently, ”The truth was I didn’t play the game. I was too much in love (with my former teacher) for seriously preparing the Concours …”

Note: French traditional name for the elitist tertiary education (first 2 or 3 years if repeat…

[Continued from previous BM Category Theory …]

$latex boxed {
text {type Algebra f a = f a} to text {a}
}&fg=aa0000&s=3$

Intuition: [Artificial Intelligence] You teach the computer, like a Primary 6 kid, that Algebra is atype of expression (f) which, after evaluation, returns a value.

If a = i (initial)[or u (terminal)],
$latex boxed {
text {(f i} to text {i )} implies
text {f = Fix-point}
}&fg=0000aa&s=3$

Intuition: Fix-point because, the Initial “i” after the evaluating the expression f, returns itself “i”.

Lambek’s Lemma
$latex boxed {
text {Endo-functor = Isomormphism}
}&fg=00aa00&s=3$

Note: Endo-functor is a functor (equivalent tofunction in Set Theory) within the same Category (Endo = Self = 自)

Video 8.1F-Algebras & Lambek’s Lemma

Video 8.2Catamorphism & Anamorphism

foldr ~ catamorphism (浅层变质) of a Fix-point endo-functor on a List.

Examples: Fibinacci, Sum_List

Replace Field scalar as in a Vector Space to Ring scalar in a Module.

Module is more powerful than Vector Space – because Ring has an “Ideal” (理想) which can partition it to Quotient Ring, but Field (scalar in a Vector Space) can’t.

Abstract Algebra studies all kinds ofmathematical structures(Group, Ring, Vector Space, Category, …) , and relationship between them if the structures are preserved after mapping.

[Hint]:

$latex (a + x)^{frac {1}{3}} + (a – x)^{frac {1}{3}} = 2(a)^{frac {1}{3}} + 2(x)^{frac {1}{3}} $

Terence Tao:

• Weakness in Math: Algebraic Topology
• Collaborative & “Lone Wolf”
• Not attempting the Riemann Hypothese: tools not there yet.

3 Phases of Math Training:

1. Pre-rigourous: intuition
2. Rigorous: formal prove
3. Post-rigourous: 1 + 2

This question was submitted by West Germany to the IMO Committee, the examiners could not solve it in 6 hours.

In the IMO (1988) only 11 contestants solved it, one of them proved it elegantly. Terence Tao (Australia) only got 1 mark out of 7 in this question.

Solution:

https://www.wired.com/2017/04/elusive-math-proof-found-almost-lost

$latex boxed {P (a + b) geq P (a) times P (b)}&fg=aa0000&s=3$

Case “=” : if (a, b) independent
Case “>” : if (a, b) dependent

Thomas Royen used only high-school math (function, derivative) in his proof in 2014. He then published it in arxiv.org website – likePerelman did with the “Poincaré Conjecture”.

Answer : (scroll below)

.

.

.
.

.

.

.
.

.

.

.

.

.

.

.

.

.

.

.

.

Answer = 3 mins

See clearer if change person to taxi car, bun to passenger.

9 taxi cars send 9 passengers will take the SAME timing as 3 taxi cars send 3 passengers.

Adjunction is the “weakeningof Equality” in Category Theory.

Equivalence of 2 Categories if:

5.2 Adjunction definition: $latex (L, R, epsilon, eta )$ such that the 2 triangle identities below ( red and blue) exist.

6.1Prove: Let C any category, D a Set.

$latex boxed {text {C(L 1, -)} simeq text {R}}&fg=aa0000&s=3$

$latex {text {Right Adjoint R in Set category is }}&fg=aa0000&s=3$ $latex {text {ALWAYS Representable}}&fg=aa0000&s=3$

1 = Singleton in Set D

From an element in the singleton Set always ‘picks’ (via the function) an image element from the other Set, hence :
$latex boxed {text{Set (1, R c) } simeq text{Rc }}&fg=0000aa&s=3$

Examples : Product & Exponential are Right Adjoints

Note: Adjoint is a more powerful concept to understand than the universal construction of Product and Exponential.

Adjoint (伴随) Functors (函子):

https://plato.stanford.edu/entries/category-theory/

[INMO 1993]

Russian mathematician Grigori Perelman proved the Poincaré Conjecture in 7 years of solitude research in his Russian apartment - same 7 years of solitude forAndrew Wiles (The Fermat’s Last Theorem)in the Cambridge attic house andZhang Yitang 张益唐 (7-Million-Gap Twin Primes) in the “Subway” sandwich kitchen.

7 is the Perfect Number. 1 week has 7 days, according to the “Book of Genesis”, God created the universe in 6 days and rested “Sabbath” on the beautiful 7th day.

People involved in his journey:

His mother who supported his early education in Math, all the way to his international fame and adulthood —Erdös Paulalso had a mother supporting her single son in the entire Mathematical life.

Prof Hamilton who “unintentionally”gave him the inspiration of the “Ricci-flow” tool – the first key to the door of The Poincaré Conjecture.

His closed Chinese friend the MIT…

Representable Functor F of C ( a, -):

$latex boxed {(-)^{a} = text {F} iff a = text {log F}}&fg=aa0000&s=3$

4.2Yoneda Lemma

Prove :

Yoneda Lemma:
$latex text {F :: C} to text {Set}$

$latex boxed {alpha text { :: [C, Set] (C (a, -),F) } simeq text {F a}}&fg=0000aa&s=3$

$latex alpha : text {Natural Transformation}$
$latex simeq : text {(Natural) Isomorphism}$

Proof: By “Diagram chasing” below, shows that

Left-side: $latex alpha text { :: [C, Set] (C (a, -),F) } $ is indeed a (co-variant) Functor.

Right-side: Functor “F a“.

Note: When talking about the natural transformations, always mention their component “x”: $latex alpha_{x}, beta_{x}$

Yoneda Embedding (Lagatta)

Brian Beckman:

You can understand Monad without too much Category Theory.

Functional Programming = using functions to compose from small functions to very complex software (eg. Nuclear system, driverless car software…).

Advantages of Functional Programming:

• Strong Types Safety: detect bugs at compile time.
• Data Protection thru Immutability: Share data safely in Concurrent / Parallel processing.
• Software ‘Componentisation’ ie Modularity: Each function always returns the same result, ease of software reliability testing.

Each “small” function is a Monoid.
f : a -> a (from input of type ‘a‘ , returns type ‘a’)
g: a -> a

compose h from f & g : (strong TYPING !!)
h = f。g : a -> a

[Note]: Object in Category, usually called Type in Haskell, eg.’a’ = Integer)

You already know a Monoid (or Category in general) : eg Clock

1. Objects: 1 2 3 …12 (hours)
2. Arrow