On Dimensions

The dimension of a hypersphere inside a n-dimensional space = $latex boxed {n – 1}$

Examples:

Dim (Circle) in 2-dim plane = 1

As we approach near the neighborhood of the tangential point on the circle, the curvature of the circle disappears, there is no difference between the circle and the tangent line (dim = 1).

Hence, Dim (Circle) = 1

A point on a circle is determined by one independent variable only, which is the polar angle.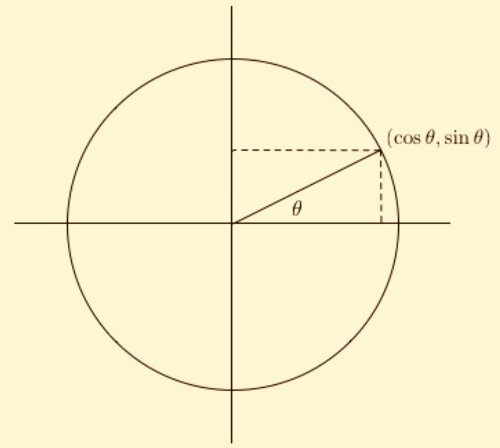

Note:
The dimension of the ambient space (2-dim plane) is not relevant to the dimension of the circle itself.

Dim (Sphere) in 3-dim Space = 2

The 2 variables (longitude, latitude) determine a position on the globe. Therefore dimension of a sphere is 2.

Interesting note:
Four Dimension Space (x, y, z, t): what we get if the 4th dimension time is fixed (frozen in time) ? We get a…