Analysis – Mathtuition88

Lebesgue’s Dominated Convergence Theorem (Continuous Version)

This is a basic but very useful corollary of the usual Lebesgue’s Dominated Convergence Theorem.

From what I see, it is basically the Sequential Criterion plus the usual Dominated Convergence Theorem.

From the book: Basic Partial Differential Equations

Arzela-Ascoli Theorem and Applications

The Arzela-Ascoli Theorem is a rather formidable-sounding theorem that gives a necessary and sufficient condition for a sequence of real-valued continuous functions on a closed and bounded interval to have a uniformly convergent subsequence.

Statement: Let $(f_n)$ be a uniformly bounded and equicontinuous sequence of real-valued continuous functions defined on a closed and bounded interval $[a,b]$ . Then there exists a subsequence $(f_{n_k})$ that converges uniformly.

The converse of the Arzela-Ascoli Theorem is also true, in the sense that if every subsequence of $(f_n)$ has a uniformly convergent subsequence, then $(f_n)$ is uniformly bounded and equicontinuous.

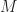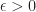Explanation of terms used: A sequence $(f_n)$ of functions on $[a,b]$ is uniformly bounded if there is a number $M$ such that $|f_n(x)|\leq M$ for all $f_n$ and all $x\in [a,b]$ . The sequence is equicontinous if, for all $\epsilon>0$ , there exists 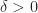$\delta>0$ such that $|f_n(x)-f_n(y)|<\epsilon$ whenever $|x-y|<\delta$ for all functions $f_n$ in the sequence. The key point here is that a single 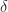$\delta$ (depending solely on $\epsilon$ ) works for the entire family of functions.

Application

Let $g:[0,1]\times [0,1]\to [0,1]$ be a continuous function and let $\{f_n\}$ be a sequence of functions such that $f_n(x)=\begin{cases}0,&0\leq x\leq 1/n\\ \int_0^{x-\frac{1}{n}}g(t,f_n(t))\ dt,&1/n\leq x\leq 1\end{cases}$

Prove that there exists a continuous function $f:[0,1]\to\mathbb{R}$ such that $f(x)=\int_0^x g(t,f(t))\ dt$ for all $x\in [0,1]$ .

The idea is to use Arzela-Ascoli Theorem. Hence, we need to show that $(f_n)$ is uniformly bounded and equicontinuous.

We have

$\begin{aligned}|f_n(x)|&\leq |\int_0^{x-\frac{1}{n}} 1\ dt|\\ &=|x-\frac{1}{n}|\\ &\leq |x|+|\frac{1}{n}|\\ &\leq 1+1\\ &=2 \end{aligned}$

This shows that the sequence is uniformly bounded.

If $0\leq x\leq 1/n$ ,

$\begin{aligned}|f_n(x)-f_n(y)|&=|0-f_n(y)|\\ &=|\int_0^{y-\frac{1}{n}} g(t,f_n(t))\ dt|\\ &\leq |\int_0^{y-\frac{1}{n}} 1\ dt|\\ &=|y-\frac{1}{n}|\\ &\leq |y-x| \end{aligned}$

Similarly if $0\leq y\leq 1/n$ , $|f_n(x)-f_n(y)|\leq |x-y|$ .

If $1/n\leq x\leq 1$ and $1/n\leq y\leq 1$ ,

$\begin{aligned}|f_n(x)-f_n(y)|&=|\int_0^{x-1/n} g(t,f_n(t))\ dt-\int_0^{y-1/n}g(t,f_n(t))\ dt|\\ &=|\int_{y-1/n}^{x-1/n}g(t,f_n(t))\ dt|\\ &\leq |\int_{y-1/n}^{x-1/n} 1\ dt|\\ &=|(x-1/n)-(y-1/n)|\\ &=|x-y| \end{aligned}$

Therefore we may choose $\delta=\epsilon$ , then whenever $|x-y|<\delta$ , $|f_n(x)-f_n(y)|\leq |x-y|<\epsilon$ . Thus the sequence is indeed equicontinuous.

By Arzela-Ascoli Theorem, there exists a subsequence $(f_{n_k})$ that is uniformly convergent.

$f_{n_k}(x)\to f(x)=\int_0^x g(t,f(t))\ dt$ .

By the Uniform Limit Theorem, $f:[0,1]\to\mathbb{R}$ is continuous since each $f_n$ is continuous.

Graph of measurable function is measurable (and has measure zero)

Let $f$ be a finite real valued measurable function on a measurable set $E\subseteq\mathbb{R}$ . Show that the set $\{(x,f(x)):x\in E\}$ is measurable.

We define $\Gamma(f,E):=\{(x,f(x)):x\in E\}$ . This is popularly known as the graph of a function. Without loss of generality, we may assume that $f$ is nonnegative. This is because we can write $f=f^+ - f^-$ , where we split the function into two nonnegative parts.

The proof here can also be found in Wheedon’s Analysis book, Chapter 5.

The strategy for proving this question is to approximate the graph of the function with arbitrarily thin rectangular strips. Let $\epsilon>0$ . Define $E_k=\{x\in E\mid \epsilon k\leq f(x)<\epsilon (k+1)\}$ , $k=0,1,2,\dots$ .

Also, $\Gamma(f,E)=\cup\Gamma(f,E_k)$ , where $\Gamma(f,E_k)$ are disjoint.

$\begin{aligned}|\Gamma(f,E)|_e&\leq\sum_{k=1}^\infty|\Gamma(f,E_k)|_e\\ &\leq\epsilon(\sum_{k=1}^\infty|E_k|)\\ &=\epsilon|E| \end{aligned}$

If $|E|<\infty$ , we can conclude $|\Gamma(f,E)|_e=0$ and thus $\Gamma(f,E)$ is measurable (and has measure zero).

If $|E|=\infty$ , we partition $E$ into countable union of sets $F_k$ each with finite measure. By the same analysis, each $\Gamma(f,F_k)$ is measurable (and has measure zero). Thus $\Gamma(f,E)=\bigcup_{k=1}^\infty\Gamma(f,F_k)$ is a countable union of measurable sets and thus is measurable (has measure zero).