Adjunction is the “weakeningof Equality” in Category Theory.
Equivalence of 2 Categories if:
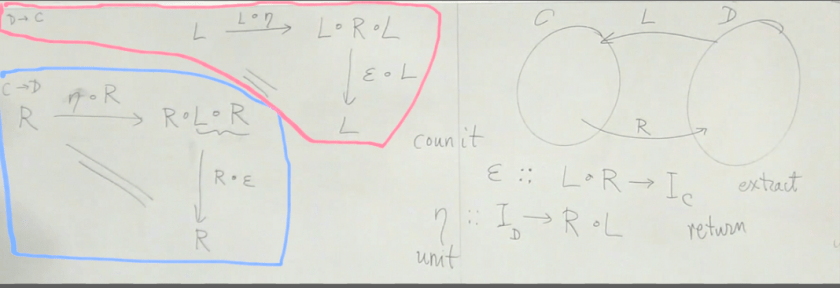
5.2 Adjunction definition: $latex (L, R, epsilon, eta )$ such that the 2 triangle identities below ( red and blue) exist.
6.1Prove: Let C any category, D a Set.
$latex boxed {text {C(L 1, -)} simeq text {R}}&fg=aa0000&s=3$
$latex {text {Right Adjoint R in Set category is }}&fg=aa0000&s=3$ $latex {text {ALWAYS Representable}}&fg=aa0000&s=3$
1 = Singleton in Set D
From an element in the singleton Set always ‘picks’ (via the function) an image element from the other Set, hence :
$latex boxed {text{Set (1, R c) } simeq text{Rc }}&fg=0000aa&s=3$
Examples : Product & Exponential are Right Adjoints
Note: Adjoint is a more powerful concept to understand than the universal construction of Product and Exponential.
Mathtuition88 