Affine Line: $latex {mathbb {A}^1}&s=3$
Six Representations of a Circle: $latex {mathbb {S}^1}&s=3$
1) Euclidean Geometry
Unit Circle : $latex x^2 + y^2 = 1$
2) Curve:
Transcendental Parameterization :
$latex boxed { e(theta) = (cos theta, sin theta) qquad
0 leq theta leq 2pi }&fg=aa0000&s=3
$
Rational Parameterisation :
$latex boxed {
e(h) = left(frac {1-h^2} {1+h^2} : , : frac {2h} {1+h^2}right) quad text { h any number or } infty
} &fg=aa0000&s=2
$
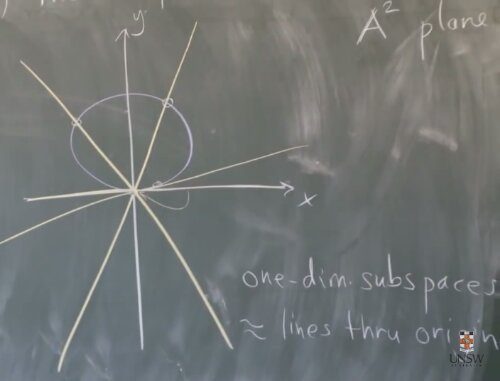
3) Affine Plane $latex {mathbb {A}^2}&s=3$
1-dim sub-Space = Lines thru Origin
4) Polygonal Representation
5) Identifying Intervals: (closed loop)
6) $latex text {Translation } (tau, {tau}^{-1}) text { on a Line } $ $latex {mathbb {A}^1}&s=3$
$latex boxed {
{mathbb {S}^1} = {mathbb {A}^1 } Big/ { langle tau , {tau}^{-1} rangle}
}&fg=aa0000&s=3
$
$latex {mathbb {S}^1} = text { Space of all orbits} $
Mathtuition88 